题目内容
15.若函数f(x)为定义在R上的奇函数,且x>0时,f(x)=lg(x+1)(1)求f(x)的解析式,并画出大致图象;
(2)若对于任意t∈R,不等式f(t2-2t)+f(k-2t2)<0恒成立,求k的取值范围.
分析 (1)由f(x)在R上为奇函数,可得f(0)=0,再由x<0,-x>0,f(x)=-f(-x),即可得到所求解析式,画出分段函数的图象;
(2)由f(x)在R上为奇函数,且为增函数,可得t2-2t<-k+2t2,再由参数分离和二次函数的最值的求法,即可得到所求k的范围.
解答 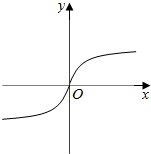 解:(1)∵f(x)为定义在R上的奇函数,
解:(1)∵f(x)为定义在R上的奇函数,
∴f(0)=0,
x<0时,-x>0,当x>0时,f(x)=lg(x+1)
则f(x)=-f(-x)=-lg(-x+1),
综上,$f(x)=\left\{\begin{array}{l}lg(x+1),x>0\\ 0,x=0\\-lg(-x+1),x<0\end{array}\right.$;
f(x)的大致图象为右图;
(2)由(1)可知f(x)在R上为增函数,
f(t2-2t)+f(k-2t2)<0⇒f(t2-2t)<-f(k-2t2)
⇒f(t2-2t)<f(-k+2t2)⇒t2-2t<-k+2t2⇒k<t2+2t恒成立,
由t2+2t=(t+1)2-1≥-1,⇒k<-1,
所以k的取值范围是(-∞-1).
点评 本题考查函数的奇偶性和单调性的判断和运用,考查不等式恒成立问题的解法,注意运用参数分离和二次函数的最值的求法,属于中档题.

练习册系列答案
相关题目
3.图中阴影部分所表示的集合是( )


| A. | (A∪B)∪(B∪C) | B. | [∁U(A∩C)]∪B | C. | (A∪C)∩(∁UB) | D. | B∩[∁U(A∪C)] |
3.已知不等式组$\left\{\begin{array}{l}{x+y-2\sqrt{2}≥0}\\{x≤2\sqrt{2}}\\{y≤2\sqrt{2}}\end{array}\right.$表示平面区域Ω,过区域Ω中的任意一个点P,作圆x2+y2=1的两条切线且切点分别为A,B,当△PAB的面积最小时,cos∠APB的值为( )
| A. | $\frac{7}{8}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
10.已知函数f(x)=lnx-$\frac{m}{x}$(m∈R)在区间[1,e]上取得最小值4,则m=( )
| A. | -3e | B. | -1 | C. | -e3 | D. | e2 |
20.某企业有4个分厂,新培训了一批6名技术人员,将这6名技术人员分配到各分厂,要求每个分厂至少1人,则不同的分配方案种数为( )
| A. | 1080 | B. | 480 | C. | 1560 | D. | 300 |
7.设x∈R,则x>1的一个必要不充分条件是( )
| A. | x>0 | B. | x<0 | C. | x>2 | D. | x<2 |
4.函数y=$\frac{1}{\sqrt{{a}^{2}-{x}^{2}}}$,那么y′等于( )
| A. | -$\frac{\sqrt{{a}^{2}-{x}^{2}}}{a}$ | B. | $\frac{1}{2}$(a2-x2)${\;}^{\frac{3}{2}}$ | C. | x(a2-x2)${\;}^{-\frac{3}{2}}$ | D. | -$\frac{1}{2}$(a2-x2)${\;}^{\frac{3}{2}}$ |