题目内容
10.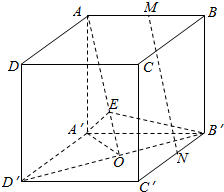 如图,在正方体ABCD-A′B′C′D'′中,O是B′D′的中点.
如图,在正方体ABCD-A′B′C′D'′中,O是B′D′的中点.(1)M、N分别是棱AB、B′C′的中点,求证:MN∥面AA′O.
(2)在线段AO上是否存在一点E,使得面A′EB′⊥面AOB′,若存在,请确定E点位置.;若不存在,请说明理由.
分析 (1)连接NO,证明MN∥AO,然后证明MN∥面AA′O.
(2)存在,点E的位置在于A′E⊥AO,交AO于点E,证明B′D′⊥A′O,B′D′⊥A′E,推出A′E⊥面AOB′,然后证明面A′EB′⊥面AOB′.
解答 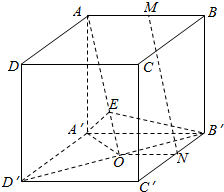 解:(1)证明:连接NO,∵AM∥ON且AM=ON,
解:(1)证明:连接NO,∵AM∥ON且AM=ON,
∴四边形AMNO是平行四边形,
∴MN∥AO,…(2分)
又∵MN?面AOA′,AO?面AOA′,
∴MN∥面AA′O.…(4分)
备注:其他方法亦可,酌情给分!
(2)存在,点E的位置在于A′E⊥AO,交AO于点E.…(6分)
证明如下:
∵O是B′D′的中点,且四边形A′B′C′D′是正方形,
∴B′D′⊥A′O,…(7分)
又∵正方体ABCD-A′B′C′D′,
∴AA′⊥面A′B′C′D′∴AA′⊥B′D′
∵AA′∩A′O=A′…(9分)
∴B′D′⊥面AA′O,
∴B′D′⊥A′E,…(11分)
∵A′E⊥AO,且AO∩OB′=O,
∴A′E⊥面AOB′,…(13分)
∵A′E?面A′EB′
∴面A′EB′⊥面AOB′.…(14分)
点评 本题考查直线与平面平行,平面与平面垂直的判定定理的应用,考查空间想象能力以及转化思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
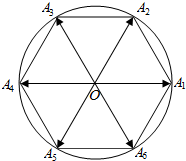 已知正六边形A1A2…A6内接于圆O,点P为圆O上一点,向量$\overrightarrow{OP}$与$\overrightarrow{O{A_i}}$的夹角为θi(i=1,2,…,6),若将θ1,θ2,…,θ6从小到大重新排列后恰好组成等差数列,则该等差数列的第3项为$\frac{5π}{12}$.
已知正六边形A1A2…A6内接于圆O,点P为圆O上一点,向量$\overrightarrow{OP}$与$\overrightarrow{O{A_i}}$的夹角为θi(i=1,2,…,6),若将θ1,θ2,…,θ6从小到大重新排列后恰好组成等差数列,则该等差数列的第3项为$\frac{5π}{12}$.