题目内容
19.设α、β都是锐角,$cosα=\frac{1}{7},cos(α+β)=\frac{{5\sqrt{3}}}{14}$,请问cosβ是否可以求解,若能求解,求出答案,若不能求解简述理由不满足余弦函数的单调性.分析 由条件利用余弦函数的单调性,得出结论.
解答 解:∵α为锐角,α+β∈(0,π),α<α+β,∵y=cosx在(0,π)上递减,∴cos(α+β)<cosα,
而已知cos(α+β)=$\frac{5\sqrt{3}}{14}$>cosα=$\frac{1}{7}$,所以条件错误,故cosβ不可解,
故答案为:不满足余弦函数的单调性.
点评 本题主要考查余弦函数的单调性,属于基础题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
9.已知两点A(1,2),B(4,-2),则与向量$\overrightarrow{AB}$共线的单位向量$\overrightarrow{e}$是( )
| A. | (3,-4) | B. | (3,-4),(-3,4) | C. | ($\frac{3}{5}$,一$\frac{4}{5}$) | D. | ($\frac{3}{5}$,一$\frac{4}{5}$),(一$\frac{3}{5}$,$\frac{4}{5}$) |
 如图,已知双曲线C的右焦点为F,过它的右顶点A作实轴的垂线,与其一条渐近线相交于点B;若双曲线C的焦距为4,△OFB为等边三角形(O为坐标原点,即双曲线C的中心),则双曲线C的方程为${x^2}-\frac{y^2}{3}=1$.
如图,已知双曲线C的右焦点为F,过它的右顶点A作实轴的垂线,与其一条渐近线相交于点B;若双曲线C的焦距为4,△OFB为等边三角形(O为坐标原点,即双曲线C的中心),则双曲线C的方程为${x^2}-\frac{y^2}{3}=1$.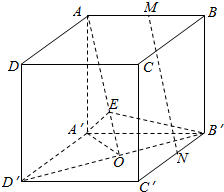 如图,在正方体ABCD-A′B′C′D'′中,O是B′D′的中点.
如图,在正方体ABCD-A′B′C′D'′中,O是B′D′的中点. 如图,已知四边形ABCD是矩形,AB=1,BC=2,PD⊥平面ABCD,且PD=3,PB的中点E,求异面直线AE与PC所成角的大小.(用反三角表示)
如图,已知四边形ABCD是矩形,AB=1,BC=2,PD⊥平面ABCD,且PD=3,PB的中点E,求异面直线AE与PC所成角的大小.(用反三角表示)