题目内容
设数列{an}的前n项和为Sn,且满足an=2-Sn(n∈N*).
(Ⅰ)求a1,a2,a3,a4的值并写出其通项公式;
(Ⅱ)设bn=nan,求数列{bn}的前n项和.
(Ⅰ)求a1,a2,a3,a4的值并写出其通项公式;
(Ⅱ)设bn=nan,求数列{bn}的前n项和.
考点:数列的求和,数列的概念及简单表示法
专题:点列、递归数列与数学归纳法
分析:(Ⅰ)由an=2-Sn,得a1,=1,a2=
,a3=
,a4=
,于是可猜想an=(
)n-1(n∈N* );
(Ⅱ)由于bn=nan=n(
)n-1,设Sn是数列数列{bn}的前n项和,利用错位相减法即可求得Sn=4-
.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2 |
(Ⅱ)由于bn=nan=n(
| 1 |
| 2 |
| n+2 |
| 2n-1 |
解答:
解:(Ⅰ)由an=2-Sn,得a1,=1,a2=
,a3=
,a4=
,
猜想an=(
)n-1(n∈N* )…(4分)
(Ⅱ)bn=nan=n(
)n-1,
设Sn是数列数列{bn}的前n项和,
Sn=1×(
)0+2×(
)1+3×(
)2+…+(n-1)×(
)n-2+n×(
)n-1,①
Sn=1×(
)1+2×(
)2+…+(n-1)×(
)n-1+n×(
)n,②
①-②得,
Sn=1+
+(
)2+…+(
)n-1+(
)n-n•(
)n
=
-n•(
)n
=2-
,
∴Sn=4-
.…(10分)
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
猜想an=(
| 1 |
| 2 |
(Ⅱ)bn=nan=n(
| 1 |
| 2 |
设Sn是数列数列{bn}的前n项和,
Sn=1×(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
①-②得,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
1-(
| ||
1-
|
| 1 |
| 2 |
=2-
| n+2 |
| 2n |
∴Sn=4-
| n+2 |
| 2n-1 |
点评:本题考查数列的求和,考查运算与猜想的能力,着重考查错位相减法求和,属于中档题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
已知函数f(x)=
,则函数y=f(x)-3的零点的个数为( )
|
| A、1 | B、2 | C、3 | D、4 |
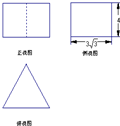 已知一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示,大致画出它的直观图,并求出它的表面积和体积.
已知一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示,大致画出它的直观图,并求出它的表面积和体积.