题目内容
6．若变量x，y满足约束条件$\left\{\begin{array}{l}y≤x\\ x+y≤1\\ y≥-1\end{array}\right.$，且z=2x+y的最大值和最小值分别为m和n，则2m-n的值为（ ）| A． | $\frac{9}{2}$ | B． | 6 | C． | $\frac{15}{2}$ | D． | 9 |
分析 作出不等式组对应的平面区域，利用线性规划的知识即可得到结论．
解答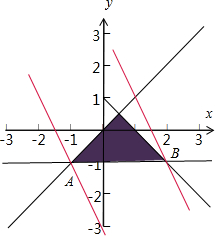 
解：作出不等式组满足约束条件$\left\{\begin{array}{l}y≤x\\ x+y≤1\\ y≥-1\end{array}\right.$的平面区域如图
由z=2x+y得y=-2x+z，
平移直线y=-2x+z，
则当直线y=-2x+z经过点B时，目标函数取得最大值，经过A时，取得最小值，由$\left\{\begin{array}{l}{y=-1}\\{y=x}\end{array}\right.$，可得A（-1，-1）时，
此时直线的截距最小，此时n=-3，
由$\left\{\begin{array}{l}{y=-1}\\{x+y=1}\end{array}\right.$，可得B（2，-1）
此时m=3，
2m-n=9．
故选：D．
点评 本题主要考查线性规划的应用，利用数形结合是解决本题的关键．
练习册系列答案
相关题目
16．一个底面是正三角形的三棱柱的正视图如图所示，则其体积等于（ ）
．
．| A． | 2$\sqrt{3}$ | B． | 4$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{2\sqrt{3}}{3}$ |
17．在平行四边形ABCD中，O是对角线的交点，E是边CD上一点，且CE=$\frac{1}{3}$CD，$\overrightarrow{OE}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$，则m+n=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{3}{4}$ | D． | $\frac{5}{6}$ |
11．已知抛物线y2=2px（p＞0），过其焦点且斜率为2的直线交抛物线于A，B两点，若线段AB的中点的纵坐标为1，则该抛物线的准线方程为（ ）
| A． | x=1 | B． | x=-1 | C． | x=2 | D． | x=-2 |
如图，建立平面直角坐标系xoy，x轴在地平面上，y轴垂直于地平面，单位长度为1千米．某炮位于坐标原点．已知炮弹发射后的轨迹在方程y=kx-$\frac{1}{20}$（1+k2）x2（k＞0）表示的曲线上，其中k与发射方向有关．炮的射程是指炮弹落地点的横坐标．