题目内容
18.求下列各曲线的标准方程(1)焦点是椭圆16x2+9y2=144的左顶点的抛物线;
(2)与双曲线$\frac{y^2}{{{5^{\;}}}}-\frac{x^2}{5}=1$共渐进线且过点$(1,\sqrt{3})$的双曲线.
分析 (1)设抛物线的标准方程为y2=-2px(p>0),其焦点坐标为$(-\frac{p}{2},0)$,则$\frac{p}{2}=3$,由此能求出抛物线的标准方程.
(2)由已知可设双曲线的标准方程为$\frac{y^2}{{{5^{\;}}}}-\frac{x^2}{5}=λ(λ≠0)$,将点$(1,\sqrt{3})$代入,能求出双曲线的标准方程.
解答 解:(1)由已知,椭圆的标准方程为$\frac{x^2}{9}+\frac{y^2}{16}=1$,其左顶点为(-3,0),
设抛物线的标准方程为y2=-2px(p>0),其焦点坐标为$(-\frac{p}{2},0)$,
则$\frac{p}{2}=3$,即p=6,
所以抛物线的标准方程为y2=-12x.…(5分)
(2)由已知可设双曲线的标准方程为$\frac{y^2}{{{5^{\;}}}}-\frac{x^2}{5}=λ(λ≠0)$
将点$(1,\sqrt{3})$代入该方程,得:$\frac{{{{({\sqrt{3}})}^2}}}{{{5^{\;}}}}-\frac{{{1^{\;}}}}{5}=λ$,解得$λ=\frac{2}{5}$
所以双曲线的标准方程为$\frac{y^2}{{{5^{\;}}}}-\frac{x^2}{5}=\frac{2}{5}$,即$\frac{y^2}{2}-\frac{x^2}{2}=1$….…(10分)
点评 本题考查抛物线方程的求法,考查双曲线方程的求法,是中档题,解题时要认真审题,注意椭圆、抛物线、双曲线性质的合理运用.

练习册系列答案
相关题目
9.已知某大城市对每人车流量拥挤等级规定如表:
该城市对国庆节7天的车流量作出如下表的统计数据:
(1)某人国庆节连续2天到该城市游玩,求这2天他遇到的车流量拥挤等级均为严重拥挤的概率;
(2)从国庆节期间随机选取2天,记这2天该城市车流量拥挤等级不是“严重拥挤”的天数为X,求X的分布列及数学期望.
| 车流量(万辆) | 0~10 | 11~50 | 51~70 | 71~80 | 81~100 | >100 |
| 拥挤等级 | 优 | 良 | 轻度拥挤 | 中度拥挤 | 重度拥挤 | 严重拥挤 |
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 107日 |
| 车流量(万辆) | 120 | 110 | 85 | 75 | 60 | 105 | 110 |
(2)从国庆节期间随机选取2天,记这2天该城市车流量拥挤等级不是“严重拥挤”的天数为X,求X的分布列及数学期望.
8.椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)和圆x2+y2=($\frac{b}{2}$t+$\frac{c}{2}$)2,(c为椭圆的半焦距)对任意t∈[1,2]恒有四个不同的交点,则椭圆的离心率e的取值范围为( )
| A. | (0,$\frac{4}{5}$] | B. | ($\frac{4}{5}$,1) | C. | (0,$\frac{\sqrt{2}}{2}$] | D. | ($\frac{\sqrt{2}}{2}$,$\frac{4}{5}$) |
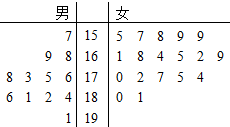 某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试立定跳远的成绩用茎叶图表示如图(单位:cm):
某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试立定跳远的成绩用茎叶图表示如图(单位:cm): 已知椭圆Γ:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率等于$\frac{{\sqrt{2}}}{2}$,椭圆Γ上的点到它的中心的距离的最小值为2.
已知椭圆Γ:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率等于$\frac{{\sqrt{2}}}{2}$,椭圆Γ上的点到它的中心的距离的最小值为2.