��Ŀ����
3��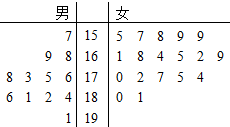 ijСѧ�����꼶��ѧ���������ʲ��ԣ���֪����һ���ѧ��30�ˣ�����������Զ�ijɼ��þ�Ҷͼ��ʾ��ͼ����λ��cm����
ijСѧ�����꼶��ѧ���������ʲ��ԣ���֪����һ���ѧ��30�ˣ�����������Զ�ijɼ��þ�Ҷͼ��ʾ��ͼ����λ��cm���������ɼ���175cm���ϣ�����175cm������Ϊ���ϸ��ɼ���175cm���£�������175cm������Ϊ�����ϸ�
Ů���ɼ���165cm���ϣ�����165cm������Ϊ���ϸ��ɼ���165cm���£�������165cm������Ϊ�����ϸ�
����������һ���Ů��������Զ�ɼ�����λ����
����������һ�������������ѡȡ3�ˣ���������2�˵ijɼ��Ǻϸ�ĸ��ʣ�
������������һ��ɼ����ϸ�ѧ����ѡȡ2�˲μӸ��ԣ���X��ʾ����������������д��X�ķֲ��У�����X����ѧ������
���� ��I���ɾ�Ҷͼ���������һ���Ů��������Զ�ɼ�����λ����
��II���衰�������˵ijɼ��ϸ�Ϊ�¼�A���������˵ijɼ��ϸ�Ϊ�¼�B�����������˵ijɼ��Ǻϸ�ĸ��ʣ�P=P��A��+P��B�����ɴ������������2�˵ijɼ��Ǻϸ�ĸ��ʣ�
��III����ΪŮ������18�ˣ�������10�˺ϸ������⣬X��ȡֵΪ0��1��2���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к�X����ѧ������
��� �⣺��I���ɾ�Ҷͼ������һ���Ů��������Զ�ɼ�����λ��Ϊ$\frac{165+168}{2}=166.5$cm������2�֣�
��II���衰�������˵ijɼ��ϸ�Ϊ�¼�A���������˵ijɼ��ϸ�Ϊ�¼�B��
���������˵ijɼ��Ǻϸ�ĸ��ʣ�P=P��A��+P��B����
��������12�ˣ�������8�˺ϸӶ�$P��A��=\frac{C_4^1•C_8^2}{{C{\;}_{12}^3}}$����4�֣�
$P��B��=\frac{C_8^3}{{C{\;}_{12}^3}}$������$p=\frac{42}{55}$����6�֣�
��III����ΪŮ������18�ˣ�������10�˺ϸ�
�����⣬X��ȡֵΪ0��1��2��
��$P��X=0��=\frac{{C_8^0C_{10}^2}}{{C_{18}^2}}=\frac{5}{17}$��
$P��X=1��=\frac{{C_8^1C_{10}^1}}{{C_{18}^2}}=\frac{80}{153}$��
$P��X=2��=\frac{{C_8^2C_{10}^0}}{{C_{18}^2}}=\frac{28}{153}$��
��ÿ��1�֣���10�֣�
��ˣ�X�ķֲ������£�
| X | 0 | 1 | 2 |
| P | $\frac{5}{17}$ | $\frac{80}{153}$ | $\frac{28}{153}$ |
�����ǣ���ΪX���ӳ����ηֲ�������$E��X��=2��\frac{8}{18}=\frac{8}{9}$���ˣ���
���� ���⿼����λ�������ʡ��ֲ��е������е��⣬����ʱҪ�������⣬ע���������֪ʶ�ĺ������ã�

 ���������ν�ϵ�д�
���������ν�ϵ�д�| A�� | $\frac{7}{25}$ | B�� | -$\frac{7}{25}$ | C�� | -$\frac{24}{25}$ | D�� | $\frac{24}{25}$ |
 ��ͼ����P��������ABCD-A1B1C1D1�ı������˶�����P��ֱ��BC��ֱ��C1D1�ľ�����ȣ��������������ƽ����չ������ô����P�Ĺ켣��չ��ͼ�е���״�ǣ�������
��ͼ����P��������ABCD-A1B1C1D1�ı������˶�����P��ֱ��BC��ֱ��C1D1�ľ�����ȣ��������������ƽ����չ������ô����P�Ĺ켣��չ��ͼ�е���״�ǣ�������


