题目内容
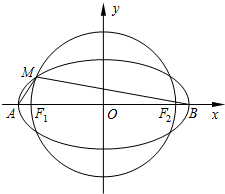如图，在平面直角坐标系xOy中，椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 4 |
（1）求椭圆的离心率；
（2）若点M又在以线段F1F2为直径的圆上，且△MAB的面积为
2
| ||
| 3 |
求椭圆的方程．
考点：直线与圆锥曲线的综合问题
专题：圆锥曲线中的最值与范围问题
分析：（1）A（-a，0），B（a，0），设M（x0，y0），由MA，MB的斜率之积为-
，得到a2=4b2．由此能注出椭圆的离心率．
（2）设M（x0，y0），由已知条件推导出x02+4y02=a2，x02+y02=
a2，y02=
，由此能求出椭圆C的标准方程．
| 1 |
| 4 |
（2）设M（x0，y0），由已知条件推导出x02+4y02=a2，x02+y02=
| 3 |
| 4 |
| 4 |
| 3a2 |
解答：
解：（1）∵椭圆
+
=1（a＞b＞0）的左、右顶点分别为A，B，
∴A（-a，0），B（a，0），
设M（x0，y0），则
+
=1．
∴kMA•kMB=
•
=
=
=-
，…（4分）
∵MA，MB的斜率之积为-
，∴a2=4b2．
∵a2=b2+c2，∴a2=4（a2-c2）．∴e2=
，
∴椭圆的离心率e=
．…（6分）
（2）设M（x0，y0），则
+
=1．
由（1）知b2=
a2，∴
+
=1，
即x02+4y02=a2．①…（8分）
∵点M又在以线段F1F2为直径的圆上，∴x02+y02=c2，
∵c2=
a2，∴x02+y02=
a2．②…（10分）
又∵S△MAB=
•2a•|y0| =a|y0| =
，
∴y02=
．③…（12分）
由①，②，③，解得a2=4．
∴椭圆C的标准方程为
+y2=1．…（14分）
| x2 |
| a2 |
| y2 |
| b2 |
∴A（-a，0），B（a，0），
设M（x0，y0），则
| x02 |
| a2 |
| y02 |
| b2 |
∴kMA•kMB=
| y0 |
| x0+a |
| y0 |
| x0-a |
| y02 |
| x02-a2 |
b2(1-
| ||
| x02-a2 |
| b2 |
| a2 |
∵MA，MB的斜率之积为-
| 1 |
| 4 |
∵a2=b2+c2，∴a2=4（a2-c2）．∴e2=
| 3 |
| 4 |
∴椭圆的离心率e=
| ||
| 2 |
（2）设M（x0，y0），则
| x02 |
| a2 |
| y02 |
| b2 |
由（1）知b2=
| 1 |
| 4 |
| x02 |
| a2 |
| 4y02 |
| a2 |
即x02+4y02=a2．①…（8分）
∵点M又在以线段F1F2为直径的圆上，∴x02+y02=c2，
∵c2=
| 3 |
| 4 |
| 3 |
| 4 |
又∵S△MAB=
| 1 |
| 2 |
2
| ||
| 3 |
∴y02=
| 4 |
| 3a2 |
由①，②，③，解得a2=4．
∴椭圆C的标准方程为
| x2 |
| 4 |
点评：本题考查椭圆的离心率的求法，考查椭圆的标准方程的求法，解题时要认真审题，注意函数与方程思想的合理运用．
练习册系列答案
相关题目