题目内容
10.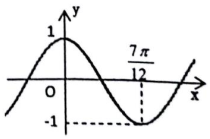 设函数y=sinωx(ω>0)的最小正周期是T,将其图象向左平移$\frac{1}{4}$T后,得到的图象如图所示,则函数y=sinωx(ω>0)的单增区间是( )
设函数y=sinωx(ω>0)的最小正周期是T,将其图象向左平移$\frac{1}{4}$T后,得到的图象如图所示,则函数y=sinωx(ω>0)的单增区间是( )| A. | [$\frac{7kπ}{6}$-$\frac{7π}{24}$,$\frac{7kπ}{6}$+$\frac{7π}{24}$](k∈Z) | B. | [$\frac{7kπ}{3}$-$\frac{7π}{24}$,$\frac{7kπ}{3}$+$\frac{7π}{24}$](k∈Z) | ||
| C. | [$\frac{7kπ}{3}$-$\frac{7π}{12}$,$\frac{7kπ}{3}$+$\frac{7π}{12}$](k∈Z) | D. | [$\frac{7kπ}{6}$+$\frac{7π}{24}$,$\frac{7kπ}{6}$+$\frac{21π}{24}$](k∈Z) |
分析 由题意和图象求出函数的周期,由周期公式求出ω的值,由整体思想和正弦函数的单调性求出递增区间.
解答 解:由图象得,$\frac{1}{2}$T=$\frac{7π}{12}$,则T=$\frac{7π}{6}$,
由$T=\frac{2π}{ω}=\frac{7π}{6}$得,ω=$\frac{12}{7}$,
所以y=sin$\frac{12}{7}$x,
由$-\frac{π}{2}+2kπ≤\frac{12}{7}x≤\frac{π}{2}+2kπ(k∈Z)$得,
$-\frac{7π}{24}+\frac{7}{6}kπ≤x≤\frac{7π}{24}+\frac{7}{6}kπ(k∈Z)$,
所以函数的递增区间是$[-\frac{7π}{24}+\frac{7}{6}kπ,\frac{7π}{24}+\frac{7}{6}kπ](k∈Z)$,
故选:A.
点评 本题考查由图象求形如y=Asin(ωx+φ)的解析式,正弦函数的单调性,以及整体思想,属于中档题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
20.已知集合U={1,2,3,4,5,6,7},A={2,4,5,7},B={3,4,5}则(∁UA)∪B=( )
| A. | {3} | B. | {4,5} | C. | {1,3,4,5,6} | D. | {2,3,4,5,7} |
5.设i为虚数单位,复数z满足$\frac{1+i}{z}$=1-i,则复数z=( )
| A. | 2i | B. | -2i | C. | i | D. | -i |
19.已知定义在$(0,\frac{π}{2})$上的函数,f′(x)为其导函数,且$\frac{f(x)}{sinx}<\frac{{{f^'}(x)}}{cosx}$恒成立,则( )
| A. | $f(\frac{π}{2})>2f(\frac{π}{6})$ | B. | $\sqrt{3}f(\frac{π}{4})>\sqrt{2}f(\frac{π}{3})$ | C. | $\sqrt{3}f(\frac{π}{6})<f(\frac{π}{3})$ | D. | $f(1)<2f(\frac{π}{6})sin1$ |
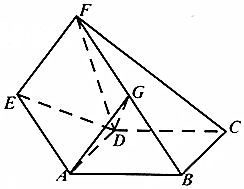 如图,已知矩形ABCD与直角梯形ABFE所在的平面互相垂直,G是BF的中点,∠AEF=∠BFE=90°,且AD=AE=EF=$\frac{1}{2}$FB=1.
如图,已知矩形ABCD与直角梯形ABFE所在的平面互相垂直,G是BF的中点,∠AEF=∠BFE=90°,且AD=AE=EF=$\frac{1}{2}$FB=1.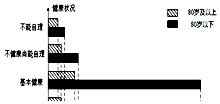 我们国家正处于老龄化社会中,老有所依也是政府的民生工程.某市共有户籍人口400万,其中老人(年龄60岁及以上)人数约有66万,为了解老人们的健康状况,政府从 老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能 自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行 统计,样本分布被制作成如图表:
我们国家正处于老龄化社会中,老有所依也是政府的民生工程.某市共有户籍人口400万,其中老人(年龄60岁及以上)人数约有66万,为了解老人们的健康状况,政府从 老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能 自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行 统计,样本分布被制作成如图表: