题目内容
在△ABC中，AB=AC=3，∠BAC=30°，CD是边AB上的高，则
•
=（ ）
| CD |
| CB |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由条件利用直角三角形中的边角关系求得CD的值，再利用两个向量的数量积的定义，求得
•
得知．
| CD |
| CB |
解答：
解：在△ABC中，AB=AC=3，∠BAC=30°，CD是边AB上的高，则有CD=AC•sin30°=
，
∴
•
=|
|•|
|•cos∠BCD=
2=
，
故选：B．
解：在△ABC中，AB=AC=3，∠BAC=30°，CD是边AB上的高，则有CD=AC•sin30°=| 3 |
| 2 |
∴
| CD |
| CB |
| CD |
| CB |
| CD |
| 9 |
| 4 |
故选：B．
点评：本题主要考查两个向量的数量积的定义，用直角三角形中的边角关系，属于基础题．
练习册系列答案
相关题目
已知三棱锥S-ABC的所有顶点都在球O的球面上，△ABC是边长为1的等边三角形，SC为球O的直径，若三棱锥S-ABC的体积为
，则球O的表面积是（ ）
| ||
| 6 |
| A、4π | ||
B、
| ||
| C、3π | ||
D、
|
已知全集U={x|2≤x≤10，且x∈N}．集合A={3，4，6，8}，B={3，5，8，9}，那么集合{2，7，10}=（ ）
| A、A∪B |
| B、A∩B |
| C、（∁UA）∩（∁UB） |
| D、（∁UA）∪（∁UB） |
已知a∈R，则“a＞2”是“a2＞4”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
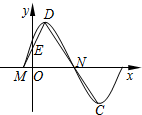右图为函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜