Question

已知三棱锥S-ABC的所有顶点都在球O的球面上，△ABC是边长为1的等边三角形，SC为球O的直径，若三棱锥S-ABC的体积为

2

6

，则球O的表面积是（　　）

• A、4π
• B、

  3

  4

  π
• C、3π
• D、

  4

  3

  π

Answer 1

考点：球的体积和表面积

专题：计算题,空间位置关系与距离

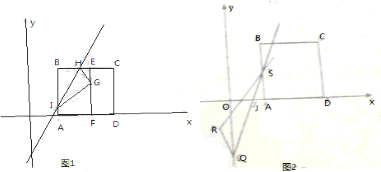
分析：根据题意作出图形，欲求球O的表面积，只须求球的半径r．利用截面圆的性质即可求出OO₁，进而求出底面ABC上的高SD，即可计算出三棱锥的体积，从而建立关于r的方程，即可求出r，从而解决问题．

解答： 解：根据题意作出图形：
设球心为O，球的半径r．过ABC三点的小圆的圆心为O₁，则OO₁⊥平面ABC，
延长CO₁交球于点D，则SD⊥平面ABC．
∵CO₁=

2

3

×

3

2

=

3

3

，
∴OO₁=

r2- 1 3

，
∴高SD=2OO₁=2

r2- 1 3

，
∵△ABC是边长为1的正三角形，
∴S_△ABC=

3

4

，
∴V_{三棱锥S-ABC}=

1

3

×

3

4

×2

r2- 1 3

=

2

6

，
∴r=1．则球O的表面积为4π
故选A．

点评：本题考查棱锥的体积，考查球内接多面体，解题的关键是确定点S到面ABC的距离．