题目内容
已知数列{an}是等差数列,数列{bn}是公比大于零的等比数列,且a1=b1=2,a3=b3=8.
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)记cn=abn,求数列{cn}的前n项和Sn.
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)记cn=abn,求数列{cn}的前n项和Sn.
考点:等差数列与等比数列的综合
专题:等差数列与等比数列
分析:(Ⅰ)设出等差数列{an}的公差为d,等比数列{bn}的公比为q,且q>0.由已知列式求得等差数列的公差和等比数列的公比,代入等差数列和等比数列的通项公式得答案;
(Ⅱ)由cn=abn结合数列{an}和{bn}的通项公式得到数列{cn}的通项公式,结合等比数列的前n项和求得数列{cn}的前n项和Sn.
(Ⅱ)由cn=abn结合数列{an}和{bn}的通项公式得到数列{cn}的通项公式,结合等比数列的前n项和求得数列{cn}的前n项和Sn.
解答:
解:(Ⅰ)设等差数列{an}的公差为d,等比数列{bn}的公比为q,且q>0.
由a1=2,a3=8,得8=2+2d,解得d=3.
∴an=2+(n-1)×3=3n-1,n∈N*.
由b1=2,b3=8,得8=2q2,又q>0,解得q=2.
∴bn=2×2n-1=2n,n∈N*;
(Ⅱ)∵cn=abn=3×2n-1,
∴Sn=3×
-n=3×2n+1-n-6.
由a1=2,a3=8,得8=2+2d,解得d=3.
∴an=2+(n-1)×3=3n-1,n∈N*.
由b1=2,b3=8,得8=2q2,又q>0,解得q=2.
∴bn=2×2n-1=2n,n∈N*;
(Ⅱ)∵cn=abn=3×2n-1,
∴Sn=3×
| 2(1-2n) |
| 1-2 |
点评:本题考查了等差数列与等比数列的通项公式,考查了等比数列的前n项和,是中档题.

练习册系列答案
相关题目
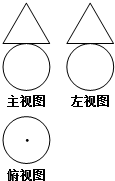 某几何体三视图如图所示,其中三角形的三边长与圆的直径均为2,则该几何体体积为( )
某几何体三视图如图所示,其中三角形的三边长与圆的直径均为2,则该几何体体积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
平行四边形ABCD中,∠CBA=120°,AD=4,对角线BD=2
,将其沿对角线BD折起,使平面ABD⊥平面BCD,若四面体ABCD顶点在同一个球面上,则该球的体积为( )
| 3 |
A、
| ||||
B、
| ||||
C、32
| ||||
| D、2π |
设定义域为(0,+∞)的单调函数f(x),对任意的x∈(0,+∞),都有f[f(x)-lnx]=e+1,若x0是方程f(x)-f′(x)=e的一个解,则x0可能存在的区间是( )
| A、(0,1) |
| B、(e-1,1) |
| C、(0,e-1) |
| D、(1,e) |