题目内容
设定义域为（0，+∞）的单调函数f（x），对任意的x∈（0，+∞），都有f[f（x）-lnx]=e+1，若x0是方程f（x）-f′（x）=e的一个解，则x0可能存在的区间是（ ）
| A、（0，1） |
| B、（e-1，1） |
| C、（0，e-1） |
| D、（1，e） |
考点：函数零点的判定定理,导数的运算
专题：函数的性质及应用
分析：由题意知：f（x）-lnx为常数，令f（x）-lnx=k（常数），则f（x）=lnx+k．由f[f（x）-lnx]=e+1，得f（k）=e+1，又f（k）=lnk+k=e+1，
所以f（x）=lnx+e，再用零点存在定理验证，
所以f（x）=lnx+e，再用零点存在定理验证，
解答：
解：由题意知：f（x）-lnx为常数，令f（x）-lnx=k（常数），则f（x）=lnx+k．
由f[f（x）-lnx]=e+1，得f（k）=e+1，又f（k）=lnk+k=e+1，
所以f（x）=lnx+e，
f′（x）=
，x＞0．
∴f（x）-f′（x）=lnx-
+e，
令g（x）=lnx-
+-e=lnx-
，x∈（0，+∞）
可判断：g（x）=lnx-
，x∈（0，+∞）上单调递增，
g（1）=-1，g（e）=1-
＞0，
∴x0∈（1，e），g（x0）=0，
∴x0是方程f（x）-f′（x）=e的一个解，则x0可能存在的区间是（1，e）
故选：D．
由f[f（x）-lnx]=e+1，得f（k）=e+1，又f（k）=lnk+k=e+1，
所以f（x）=lnx+e，
f′（x）=
| 1 |
| x |
∴f（x）-f′（x）=lnx-
| 1 |
| x |
令g（x）=lnx-
| 1 |
| x |
| 1 |
| x |
可判断：g（x）=lnx-
| 1 |
| x |
g（1）=-1，g（e）=1-
| 1 |
| e |
∴x0∈（1，e），g（x0）=0，
∴x0是方程f（x）-f′（x）=e的一个解，则x0可能存在的区间是（1，e）
故选：D．
点评：本题考查了函数的单调性，零点的判断，构造思想，属于中档题．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
若平面向量
，
满足|
+
|=1，且
=2
，则|
|=（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| b |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
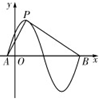函数y=sin（πx+φ）（φ＞0）的部分图象如图所示，设P是图象的最高点，A，B是图象与x轴的交点，把∠APB=θ，则tanθ的值是（ ）