题目内容
已知函数f(x)=x2-2ax+2,当x0∈[1,+∞)时,恒有f(x0)>0,求实数a的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:先求出二次函数f(x)的对称轴x=a,所以讨论a≤1和a>1两种情况,根据二次函数的单调性或取得顶点情况求出f(x)在[1,+∞)的最小值,所以只要该最小值大于0即可,这样便可求出实数a的取值范围.
解答:
解:f(x)的对称轴为x=a;
∴(1)a≤1时,f(x)在[1,+∞)上单调递增;
∴f(x)在[1,+∞)上的最小值为f(1)=3-2a;
根据题意则有:3-2a>0,a<
;
∴此时a≤1;
(2)a>1时,f(x)在[1,+∞)上的最小值为f(a)=-a2+2;
∴便有-a2+2>0;
解得-
<a<
;
∴此时1<a<
;
综上得实数a的取值范围为(-∞,
).
∴(1)a≤1时,f(x)在[1,+∞)上单调递增;
∴f(x)在[1,+∞)上的最小值为f(1)=3-2a;
根据题意则有:3-2a>0,a<
| 3 |
| 2 |
∴此时a≤1;
(2)a>1时,f(x)在[1,+∞)上的最小值为f(a)=-a2+2;
∴便有-a2+2>0;
解得-
| 2 |
| 2 |
∴此时1<a<
| 2 |
综上得实数a的取值范围为(-∞,
| 2 |
点评:考查二次函数的对称轴,二次函数的单调性,以及二次函数的顶点,二次函数的最值.

练习册系列答案
相关题目
已知三棱锥S-ABC的体积为V,D,E,F,分别是棱SB,BC,SC的中点,三棱锥A-DEF体积为V1,则
=( )
| V1 |
| V |
A、
| ||
B、
| ||
C、
| ||
D、
|
若平面向量
,
满足|
+
|=1,且
=2
,则|
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
| b |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
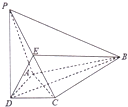 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥DC,DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥DC,DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2 如图,正方体ABCD-A1B1C1D1中,E为DD1的中点.
如图,正方体ABCD-A1B1C1D1中,E为DD1的中点.