题目内容
设i为虚数单位,则复数z=
在复平面内对应的点在( )
| i2014 |
| 1-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:利用虚数单位i的运算性质化简分子,然后利用复数代数形式的除法运算化简,求出复数z对应点的坐标得答案.
解答:
解:∵z=
=
=
=
=-
-
,
∴复数z在复平面内对应的点的坐标为(-
,-
),在第三象限.
故选:C.
| i2014 |
| 1-i |
| (i2)1007 |
| 1-i |
| -1 |
| 1-i |
| -(1+i) |
| (1-i)(1+i) |
| 1 |
| 2 |
| i |
| 2 |
∴复数z在复平面内对应的点的坐标为(-
| 1 |
| 2 |
| 1 |
| 2 |
故选:C.
点评:本题考查复数代数形式的除法运算,考查了虚数单位i的运算性质,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知实数x,y满足
,则目标函数z=2x-y-1的最大值为( )
|
| A、5 | ||
| B、4 | ||
C、
| ||
| D、-3 |
在复平面内,复数z=
的虚部为( )
| 5i |
| 2i-1 |
| A、1 | B、-1 | C、i | D、-i |
设复数z=
,则z的共轭复数
为( )
| 1-i |
| 1+i |
. |
| z |
| A、1 | B、-1 | C、-i | D、i |
已知2弧度的圆心角所对的弦长为2,那么此圆心角所夹扇形的面积为( )
A、
| ||
B、
| ||
C、
| ||
| D、tan1 |
已知a=log23,b=ln2,c=5 -
,则a,b,c的大小关系是( )
| 1 |
| 2 |
| A、a>c>b |
| B、a>b>c |
| C、b>a>c |
| D、b>c>a |
已知函数f(x)=kx+1,其中实数k随机取自区间[-2,1],则对于?x∈[-1,1],都有f(x)≥0恒成立的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
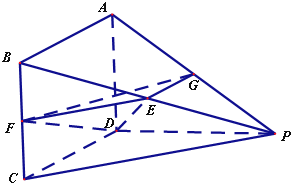 如图,在四棱锥P-ABCD中,四边形ABCD是正方形,CD=PD,∠ADP=90°,∠CDP=120°,E,F,G分别为PB,BC,AP的中点.
如图,在四棱锥P-ABCD中,四边形ABCD是正方形,CD=PD,∠ADP=90°,∠CDP=120°,E,F,G分别为PB,BC,AP的中点.