题目内容
设F1,F2分别为双曲线
-
=1(a>0,b>0)的左、右焦点,双曲线上存在一点P使得(|PF1|-|PF2|)2=b2-3ab,则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
| C、4 | ||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据(|PF1|-|PF2|)2=b2-3ab,由双曲线的定义可得(2a)2=b2-3ab,求得a=
,c=
=
b,即可求出双曲线的离心率.
| b |
| 4 |
| a2+b2 |
| ||
| 4 |
解答:
解:∵(|PF1|-|PF2|)2=b2-3ab,
∴由双曲线的定义可得(2a)2=b2-3ab,
∴4a2+3ab-b2=0,
∴a=
,
∴c=
=
b,
∴e=
=
.
故选:D.
∴由双曲线的定义可得(2a)2=b2-3ab,
∴4a2+3ab-b2=0,
∴a=
| b |
| 4 |
∴c=
| a2+b2 |
| ||
| 4 |
∴e=
| c |
| a |
| 17 |
故选:D.
点评:本题主要考查了双曲线的简单性质,考查学生的计算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设α∈(0,
),β∈(0,
),且tanα=
,则( )
| π |
| 2 |
| π |
| 2 |
| 1+sinβ |
| cosβ |
A、3α-β=
| ||
B、3α+β=
| ||
C、2α-β=
| ||
D、2α+β=
|
在如图所示的空间直角坐标系O-xyz中,一个四面体的顶点坐标分别为(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出的编号为①,②,③,④的四个图,则该四面体的正视图和俯视图分别为( )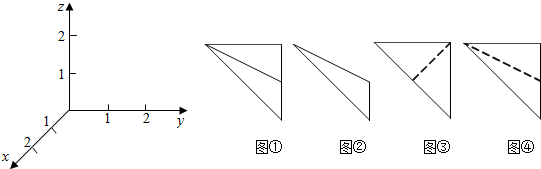

| A、①和② | B、③和① |
| C、④和③ | D、④和② |
已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2-3x,则函数g(x)=f(x)-x+3的零点的集合为( )
| A、{1,3} | ||
| B、{-3,-1,1,3} | ||
C、{2-
| ||
D、{-2-
|