题目内容
已知抛物线C：y2=8x的焦点为F，准线为l，P是l上一点，Q是直线PF与C的一个交点，若
=4
，则|QF|=（ ）
| FP |
| FQ |
A、
| ||
| B、3 | ||
C、
| ||
| D、2 |
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：求得直线PF的方程，与y2=8x联立可得x=1，利用|QF|=d可求．
解答：
解：设Q到l的距离为d，则|QF|=d，
∵
=4
，
∴|PQ|=3d，
∴不妨设直线PF的斜率为-2
，
∵F（2，0），
∴直线PF的方程为y=-2
（x-2），
与y2=8x联立可得x=1，
∴|QF|=d=1+2=3，
故选：B．
∵
| FP |
| FQ |
∴|PQ|=3d，
∴不妨设直线PF的斜率为-2
| 2 |
∵F（2，0），
∴直线PF的方程为y=-2
| 2 |
与y2=8x联立可得x=1，
∴|QF|=d=1+2=3，
故选：B．
点评：本题考查抛物线的简单性质，考查直线与抛物线的位置关系，属于基础题．
练习册系列答案
相关题目
已知向量
=（k，3），
=（1，4），
=（2，1）且（2
-3
）⊥
，则实数k=（ ）
| a |
| b |
| c |
| a |
| b |
| c |
A、-
| ||
| B、0 | ||
| C、3 | ||
D、
|
下列叙述中正确的是（ ）
| A、若a，b，c∈R，则“ax2+bx+c≥0”的充分条件是“b2-4ac≤0” |
| B、若a，b，c∈R，则“ab2＞cb2”的充要条件是“a＞c” |
| C、命题“对任意x∈R，有x2≥0”的否定是“存在x∈R，有x2≥0” |
| D、l是一条直线，α，β是两个不同的平面，若l⊥α，l⊥β，则α∥β |
设函数f（x），g（x）的定义域都为R，且f（x）是奇函数，g（x）是偶函数，则下列结论中正确的是（ ）
| A、f（x）g（x）是偶函数 |
| B、|f（x）|g（x）是奇函数 |
| C、f（x）|g（x）|是奇函数 |
| D、|f（x）g（x）|是奇函数 |
设F1，F2分别为双曲线
-
=1（a＞0，b＞0）的左、右焦点，双曲线上存在一点P使得（|PF1|-|PF2|）2=b2-3ab，则该双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
| C、4 | ||
D、
|
随机掷两枚质地均匀的骰子，它们向上的点数之和不超过5的概率记为p1，点数之和大于5的概率记为p2，点数之和为偶数的概率记为p3，则（ ）
| A、p1＜p2＜p3 |
| B、p2＜p1＜p3 |
| C、p1＜p3＜p2 |
| D、p3＜p1＜p2 |
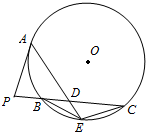如图，P是⊙O外一点，PA是切线，A为切点，割线PBC与⊙O相交于点B，C，PC=2PA，D为PC的中点，AD的延长线交⊙O于点E，证明：