题目内容
9.设f(x)是定义在R上的最小正周期为$\frac{7π}{6}$的函数,且在$[-\frac{5π}{6},\frac{π}{3})$上$f(x)=\left\{\begin{array}{l}sinx,x∈[-\frac{5π}{6},0)\\ cosx+a,x∈[0,\frac{π}{3}]\end{array}\right.$,则a=-1,$f(-\frac{16π}{3})$=$-\frac{{\sqrt{3}}}{2}$.分析 根据函数的周期,可得$f(\frac{π}{3})=f(-\frac{5π}{6})$,进而得到a值,将x=$-\frac{16π}{3}$代入可得答案.
解答 解:由于f(x)的周期为$\frac{7π}{6}$,则$f(\frac{π}{3})=f(-\frac{5π}{6})$,即$cos\frac{π}{3}+a=sin(-\frac{5π}{6})$,
解得a=-1.
此时$f(-\frac{16π}{3})=f(-\frac{2π}{3})=sin(-\frac{2π}{3})=-\frac{{\sqrt{3}}}{2}$.
故答案为:-1;$-\frac{{\sqrt{3}}}{2}$.
点评 本题考查的知识点是分段函数的应用,函数求值,函数的周期性,难度中档.

练习册系列答案
相关题目
4.已知数列{an}的首项a1=1,前n项和为Sn,且满足2an+1+Sn=2,则满足$\frac{1001}{1000}<\frac{{{S_{2n}}}}{S_n}<\frac{11}{10}$的n的最大值是( )
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
18.设$a=\sqrt{3},b=\sqrt{15}-\sqrt{7},c=\sqrt{11}-\sqrt{3}$,那么a,b,c的大小关系是( )
| A. | a>b>c | B. | a>c>b | C. | b>a>c | D. | b>c>a |

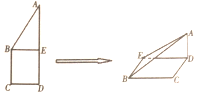 如图所示,正方形BCDE的边长为a,已知$AB=\sqrt{3}BC$,将△ABE沿BE边折起,折起后A点在平面BCDE上的射影为D点,则翻折后的几何体中有如下描述:
如图所示,正方形BCDE的边长为a,已知$AB=\sqrt{3}BC$,将△ABE沿BE边折起,折起后A点在平面BCDE上的射影为D点,则翻折后的几何体中有如下描述: