题目内容
一个袋中装有大小质地相同的20个小球,其中红球与白球各10个,若一人从袋中连续两次摸球,一次摸出一个小球(第一次摸出小球不放回),则在第一次摸出1个红球的条件下,第二次摸出1个白球的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:概率与统计
分析:在第一次摸出1个红球的条件下,袋中有19个球,其中白球10个,故可求出第二次摸出1个白球的概率
解答:
解:在第一次摸出1个红球的条件下,袋中有19个球,其中白球10个,故第二次摸出1个白球的概率为
,
故选:C
| 10 |
| 19 |
故选:C
点评:本题考查了概率的计算方法,看准确事件之间的联系,正确运用公式,是解决本题的关键.

练习册系列答案
相关题目
双曲线
-
=1的两个焦点为F1(-5,0),F2(5,0),其上一点M满足MF1-MF2=-8,则该双曲线的一条渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、4x+3y=0 |
| B、4x-5y=0 |
| C、3x-4y=0 |
| D、5x+3y=0 |
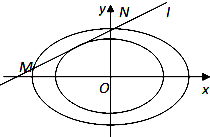 已知中心在原点O,左焦点为F1(-1,0)的椭圆C的左顶点为A,上顶点为B,F1到直线AB的距离为
已知中心在原点O,左焦点为F1(-1,0)的椭圆C的左顶点为A,上顶点为B,F1到直线AB的距离为