题目内容
设a>0,x∈[-1,1]时,函数y=-x2-ax+b有最小值-1,最大值1,求使函数取得最小值和最大值时相应的x值.
考点:二次函数的性质
专题:计算题,函数的性质及应用
分析:由题意判断二次函数图象的开口方向及对称轴,并由对称轴进行讨论.
解答:
解:函数y=-x2-ax+b的图象开口向下,对称轴为x=-
<0,
①当-
≤-1,即a≥2时,
函数y=-x2-ax+b在[-1,1]上单调上单调递减,
函数y=-x2-ax+b在x=-1时取得最大值,在x=1时取得最小值.
①当-
>-1,即0<a<2时,
函数y=-x2-ax+b在x=-
时取得最大值,在x=1时取得最小值.
| a |
| 2 |
①当-
| a |
| 2 |
函数y=-x2-ax+b在[-1,1]上单调上单调递减,
函数y=-x2-ax+b在x=-1时取得最大值,在x=1时取得最小值.
①当-
| a |
| 2 |
函数y=-x2-ax+b在x=-
| a |
| 2 |
点评:本题考查了二次函数的最值问题,属于基础题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
在公差为4的正项等差数列中,a3与2的算术平均值等于S3与2的几何平均值,其中S3 表示数列的前三项和,则a10为( )
| A、38 | B、40 | C、42 | D、44 |
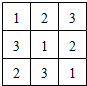 (1)如图,将1,2,3填入3×3的方格中,要求每行、每列都没有重复数字,右面是一种填法,则不同的填写方法共有几种?(用数字作答).
(1)如图,将1,2,3填入3×3的方格中,要求每行、每列都没有重复数字,右面是一种填法,则不同的填写方法共有几种?(用数字作答).