题目内容
20.已知数列{an}满足:an≠0,a1=$\frac{1}{3}$,an-an+1=2an•an+1.(n∈N*).(1)求证:{$\frac{1}{{a}_{n}}$}是等差数列,并求出an;
(2)证明:a1a2+a2a3+…+anan+1<$\frac{1}{6}$.
分析 (1)两边除以an•an+1,由等差数列的定义和通项公式,即可得证,由等差数列的通项公式即可得到;
(2)运用数列的求和方法:裂项相消求和,运用不等式的性质,即可得证.
解答 证明:(1)a1=$\frac{1}{3}$,an-an+1=2an•an+1.可得
$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=2,则{$\frac{1}{{a}_{n}}$}是首项为3,公差为2的等差数列,
$\frac{1}{{a}_{n}}$=$\frac{1}{{a}_{1}}$+2(n-1)=3+2(n-1)=2n+1,
即有an=$\frac{1}{2n+1}$;
(2)证明:a1a2+a2a3+…+anan+1=$\frac{1}{3•5}$+$\frac{1}{5•7}$+…+$\frac{1}{(2n+1)(2n+3)}$
=$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{2n+1}$-$\frac{1}{2n+3}$)
=$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{2n+3}$)=$\frac{1}{6}$-$\frac{1}{2}$•$\frac{1}{2n+3}$<$\frac{1}{6}$.
点评 本题考查等差数列的定义和通项公式的运用,考查数列的求和方法:裂项相消求和,注意运用不等式的性质,属于中档题.

练习册系列答案
相关题目
3.△ABC的三边长度分别是2,3,x,由所有满足该条件的x构成集合M,现从集合M中任取一x值,所得△ABC恰好是钝角三角形的概率为( )
| A. | $\frac{{4-\sqrt{13}+\sqrt{5}}}{4}$ | B. | $\frac{{5-\sqrt{13}}}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{{\sqrt{5}-1}}{4}$ |
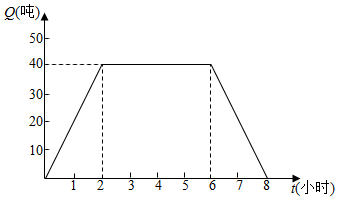 某游泳池先开进水管注水,使用完毕后开排水管排水,存水量Q(吨)与时间t(小时)之间的函数关系如图,则Q关于t的函数解析式为Q(t)=$\left\{\begin{array}{l}{20t,}&{0≤t≤2}\\{40,}&{2<t<5}\\{-\frac{40}{3}t+\frac{320}{3},}&{5<t≤8}\end{array}\right.$.
某游泳池先开进水管注水,使用完毕后开排水管排水,存水量Q(吨)与时间t(小时)之间的函数关系如图,则Q关于t的函数解析式为Q(t)=$\left\{\begin{array}{l}{20t,}&{0≤t≤2}\\{40,}&{2<t<5}\\{-\frac{40}{3}t+\frac{320}{3},}&{5<t≤8}\end{array}\right.$.