题目内容
12．设m，n∈（0，+∞），若直线（m+2）x+（n+2）y-4=0与圆（x-1）2+（y-1）2=1相切，则m+n的最小值是（ ）| A． | 4+4$\sqrt{2}$ | B． | 2+2$\sqrt{2}$ | C． | 4+$\sqrt{2}$ | D． | 4+2$\sqrt{2}$ |
分析 根据圆心到切线的距离等于半径建立关系（m-2）（n-2）=8，然后借助于基本不等式求解即可．
解答 解：由直线与圆相切可知|m+2+n+2-4|=$\sqrt{（m+2）^{2}+（n+2）^{2}}$
整理得（m-2）（n-2）=8，
由8=（m-2）（n-2）≤（$\frac{m+n-4}{2}$）2，
当且仅当m=n时等号成立，
可知m+n≥4+4$\sqrt{2}$．
故选A．
点评 本题借助基本不等式考查点到直线的距离，属于中档题
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
相关题目
3．△ABC的三边长度分别是2，3，x，由所有满足该条件的x构成集合M，现从集合M中任取一x值，所得△ABC恰好是钝角三角形的概率为（ ）
| A． | $\frac{{4-\sqrt{13}+\sqrt{5}}}{4}$ | B． | $\frac{{5-\sqrt{13}}}{4}$ | C． | $\frac{3}{4}$ | D． | $\frac{{\sqrt{5}-1}}{4}$ |
20．“α≠β”是“cosα≠cosβ”的（ ）条件．
| A． | 充分不必要 | B． | 必要不充分 | ||
| C． | 充要 | D． | 既不充分又不必要 |
如图所示的三角形数阵叫“牛顿调和三角形”，它们是由整数的倒数组成的，第n行有n个数且两端的数均为$\frac{1}{n}$（n≥2），每个数是它下一行左右相邻两数的和，如$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$，=$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$，$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$，…，
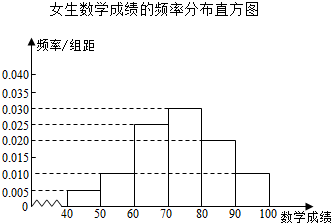
4．某校为了解高一学生的数学水平，随机抽取了高一男，女生各40人参加数学等级考试，得到男生数学成绩的频数分布表和女生数学成绩的频率分布直方图如下：
男生数学成绩的频数分布表
（Ⅰ）画出男生数学成绩的频率分布直方图，并比较该校高一男，女生数学成绩的方差大小；（只需写出结论）
（Ⅱ）根据女生数学成绩的频率分布直方图，估计该校高一女生的数学平均成绩；
（Ⅲ）依据学生的数学成绩，将学生的数学水平划分为三个等级：
估计该校高一男，女生谁的“数学水平良好”的可能性大，并说明理由．
男生数学成绩的频数分布表
| 成绩分组 | [50，60） | [60，70） | [70，80） | [80，90） | [90，100] |
| 频数 | 2 | 8 | 16 | 10 | 4 |
（Ⅰ）画出男生数学成绩的频率分布直方图，并比较该校高一男，女生数学成绩的方差大小；（只需写出结论）
（Ⅱ）根据女生数学成绩的频率分布直方图，估计该校高一女生的数学平均成绩；
（Ⅲ）依据学生的数学成绩，将学生的数学水平划分为三个等级：
| 数学成绩 | 低于70分 | 70～90分 | 不低于90分 |
| 数学水平 | 一般 | 良好 | 优秀 |
1．设p、q是两个命题．如果命题p是命题q的充分不必要条件．那么￢p是￢q的（ ）
| A． | 充要条件 | B． | 必要不充分条件 | ||
| C． | 充分不必要条件 | D． | 既不充分也不必要条件 |