题目内容

已知两个单位向量
e1
，
e2
的夹角为45°，且满足
e1
⊥（λ
e2
-
e1
），则实数λ的值为（　　）
A、1
B、
2
C、
2
3
3
D、2
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：运用向量的数量积的定义，可得两个单位向量
e1
，
e2
的数量积，再由向量垂直的条件：数量积为0，计算即可得到所求值．
解答： 解：由单位向量
e1
，
e2
的夹角为45°，
则
e1
•
e2
=1×1×cos45°=
2
2
，
由
e1
⊥（λ
e2
-
e1
），
可得，
e1
•（λ
e2
-
e1
）=0，
即λ
e1
•
e2
-
e1
2=0，
则
2
2
λ-1=0，
解得λ=
2
．
故选B．
点评：本题考查平面向量的数量积的坐标定义和性质，考查向量垂直的条件，考查运算能力，属于基础题．
练习册系列答案
相关题目
已知等差数列{an}，a6=2，则此数列的前11项的和S11=（　　）
A、44B、33C、22D、11
在锐角△ABC中，角A，B，C的对边分别为a，b，c，且
3
b=2csinB
（1）求角C的大小；
（2）若c2=（a-b）2+6，求△ABC的面积．
函数f（x）=
1
4x+m
（m＞0），x1，x2∈R，当x1+x2=1时，f（x1）+f（x2）=
1
2
．
（1）求m的值；
（2）解不等式f（log2（x-1）-1）＞f（log
1
2
（x-1）-
3
2
）．
已知向量
a
=（sinx，1），
b
（cosx，0），x∈R．
（1）当x=
π
4
时，求向量
a
+
b
的坐标；
（2）若函数f（x）=|
a
+
b
|2-m，f（0）=0，求实数m的值．
在等差数列{an}中，a1=3，公差为d，前n项和为Sn，当且仅当n=6时Sn取得最大值，则d的取值范围是
 
．
若函数y=ax+b的部分图象如图所示，则（　　）
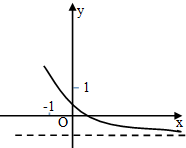
A、0＜a＜1，-1＜b＜0
B、0＜a＜1，0＜b＜1
C、a＞1，-1＜b＜0
D、a＞1，0＜b＜1
函数y=
x+3
+
1
1-x
的定义域为
 
．
已知函数f（x）=log2（1+2x+4xa），其中 a∈R．
（1）a=-2时，求函数f（x）定义域；
（2）当x∈（-∞，1]时，函数f（x）有意义，求实数a的取值范围；
（3）a=-1，函数y=f（x）-x-b（-1≤x≤0）有零点，求实数b的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网