题目内容
16.已知函数$f(x)=|x|+{2^x}-\frac{1}{2}({x<0})$与g(x)=|x|+log2(x+a)的图象上存在关于y轴对称的点,则a的取值范围是( )| A. | $({-∞,-\sqrt{2}})$ | B. | $({-∞,\sqrt{2}})$ | C. | $({-∞,2\sqrt{2}})$ | D. | $({-2\sqrt{2},\frac{{\sqrt{2}}}{2}})$ |
分析 令f(-x)=g(x)在(0,+∞)上有解,根据函数图象得出a的范围.
解答 解:f(x)关于y轴对称的函数为h(x)=f(-x)=x+2-x-$\frac{1}{2}$(x>0),
令h(x)=g(x)得2-x-$\frac{1}{2}$=log2(x+a)(x>0),
则方程2-x-$\frac{1}{2}$=log2(x+a)在(0,+∞)上有解,
作出y=2-x-$\frac{1}{2}$与y=log2(x+a)的函数图象如图所示:
当a≤0时,函数y=2-x-$\frac{1}{2}$与y=log2(x+a)的函数图象在(0,+∞)上必有交点,符合题意;
若a>0,若两图象在(0,+∞)上有交点,则log2a$<\frac{1}{2}$,解得0$<a<\sqrt{2}$,
综上,a$<\sqrt{2}$.
故选:B.
点评 本题考查了方程解与函数图象的关系,函数图象的变换,属于中档题.

练习册系列答案
相关题目
6.定义在R上的周期为2的函数,满足f(2+x)=f(2-x),在[-3,-2]上是减函数,若A,B是锐角三角形的两个内角,则( )
| A. | f(sinA)>f(cosB) | B. | f(cosB)>f(sinA) | C. | f(sinA)>f(sinB) | D. | f(cosB)>f(cosA) |
7.已知动点P(x,y)满足5$\sqrt{{(x-1)}^{2}{+(y-2)}^{2}}$=|3x+4y-1|,则点P的轨迹是( )
| A. | 直线 | B. | 抛物线 | C. | 双曲线 | D. | 椭圆 |
4.已知$f(x)=2sin({2x+\frac{π}{6}})$,若将它的图象向右平移$\frac{π}{6}$个单位,得到函数g(x)的图象,则函数g(x)图象的一条对称轴的方程为( )
| A. | $x=\frac{π}{3}$ | B. | $x=\frac{π}{4}$ | C. | $x=\frac{π}{6}$ | D. | $x=\frac{π}{12}$ |
1.已知$f(x)=\left\{{\begin{array}{l}{{2^x}-2,x≥0}\\{-{x^2}+3,x<0}\end{array}}\right.$,若f(a)=2,则a的取值为( )
| A. | 2 | B. | -1或2 | C. | ±1或2 | D. | 1或2 |
8.若函数f(x)=$\frac{{a{x^2}}}{2}-({1+2a})x+2lnx({a>0})$在区间$({\frac{1}{2},1})$内有极大值,则a的取值范围是( )
| A. | $({\frac{1}{e},+∞})$ | B. | (1,+∞) | C. | (1,2) | D. | (2,+∞) |
6.执行如图所示的程序框图,输出的n的值为( )
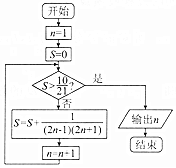

| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
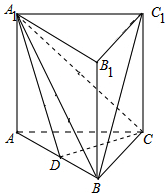 如图,在三棱柱ABC-A1B1C1中,底面△ABC是边长为2的等边三角形,D为AB中点.
如图,在三棱柱ABC-A1B1C1中,底面△ABC是边长为2的等边三角形,D为AB中点.