题目内容
6．执行如图所示的程序框图，输出的n的值为（ ）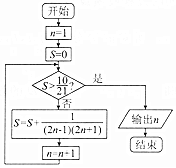
| A． | 10 | B． | 11 | C． | 12 | D． | 13 |
分析 模拟执行程序框图，求出s=$\frac{10}{21}$时n的值是11，得到n=12时，s＞$\frac{10}{21}$，输出n的值为12．
解答 解：第一次循环，s=$\frac{1}{1×3}$，n=2，
第二次循环，s=$\frac{1}{1×3}$+$\frac{1}{3×5}$，n=3，
第三次循环，s=$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$，n=4，
…，
第m次循环，s=$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{（2m-1）（2m+1）}$=$\frac{1}{2}$（1-$\frac{1}{2m+1}$）=$\frac{10}{21}$，
解得：m=10，n=m+1=11，
第m+1次循环，s＞$\frac{10}{21}$，n=12，输出n=12；
故选：C．
点评 本题主要考查了程序框图和算法，依次写出每次循环得到的S，n的值，得到第m次循环，s=$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{（2m-1）（2m+1）}$=$\frac{1}{2}$（1-$\frac{1}{2m+1}$）是解题的关键，属于基本知识的考查．
练习册系列答案
相关题目
16．已知函数$f（x）=|x|+{2^x}-\frac{1}{2}（{x＜0}）$与g（x）=|x|+log2（x+a）的图象上存在关于y轴对称的点，则a的取值范围是（ ）
| A． | $（{-∞，-\sqrt{2}}）$ | B． | $（{-∞，\sqrt{2}}）$ | C． | $（{-∞，2\sqrt{2}}）$ | D． | $（{-2\sqrt{2}，\frac{{\sqrt{2}}}{2}}）$ |
17．若实数x、y满足$\left\{\begin{array}{l}{2x-y+2≥0}\\{2x+y-6≤0}\\{0≤y≤3}\end{array}\right.$，且z=3x-y，则z的最大值为（ ）
| A． | $\frac{3}{2}$ | B． | -$\frac{3}{2}$ | C． | 9 | D． | -3 |
1．中国古代数学名著《九章算术》中记载：今有大夫、不更、簪襃、上造、公士凡五人，共猜得五鹿，欲以爵次分之，问各得几何？意思是：今有大夫、不更、簪襃、上造、公士凡五人，他们共猎获5只鹿，欲按其爵级高低依次递减相同的量来分配，问各得多少，若五只鹿的鹿肉共500斤，则不更、簪襃、上造这三人共分得鹿肉斤数为（ ）
| A． | 200 | B． | 300 | C． | $\frac{500}{3}$ | D． | 400 |
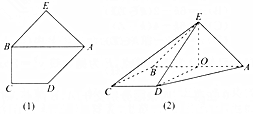如图（1），在五边形BCDAE中，CD∥AB，∠BCD=90°，CD=BC=1，AB=2，△ABE是以AB为斜边的等腰直角三角形，现将△ABE沿AB折起，使平面ABE⊥平面ABCD，如图（2），记线段AB的中点为O．
18．已知f（x）=sinx-x，命题p：?x∈（0，$\frac{π}{2}}$），f（x）＜0，则（ ）
| A． | p是假命题，￢p：：?x∈（0，$\frac{π}{2}}$），f（x）≥0 | B． | p是假命题，￢p：：?x∈（0，$\frac{π}{2}}$），f（x）≥0 | ||
| C． | P是真命题，￢p：：?x∈（0，$\frac{π}{2}}$），f（x）≥0 | D． | p是真命题，￢p：：?x∈（0，$\frac{π}{2}}$），f（x）≥0 |
