题目内容
6.定义在R上的周期为2的函数,满足f(2+x)=f(2-x),在[-3,-2]上是减函数,若A,B是锐角三角形的两个内角,则( )| A. | f(sinA)>f(cosB) | B. | f(cosB)>f(sinA) | C. | f(sinA)>f(sinB) | D. | f(cosB)>f(cosA) |
分析 由题意可得f(x)的图象关于直线x=2对称,且在[-1,0]递减,即有f(-x)=f(x),可得f(x)为偶函数,可得f(x)在[0,1]递增,由A,B是锐角三角形的两个内角,可得A+B>$\frac{π}{2}$,运用诱导公式和正弦函数的图象和性质,结合f(x)的单调性,即可得到结论.
解答 解:定义在R上的周期为2的函数,满足f(2+x)=f(2-x),在[-3,-2]上是减函数,
可得f(x)的图象关于直线x=2对称,且在[-1,0]递减,
由f(-x)=f(4+x),且f(x+4)=f(x),
即有f(-x)=f(x),可得f(x)为偶函数,
可得f(x)在[0,1]递增,
由A,B是锐角三角形的两个内角,可得A+B>$\frac{π}{2}$,
即$\frac{π}{2}$>A>$\frac{π}{2}$-B>0,
可得sinA>sin($\frac{π}{2}$-B)=cosB,
由sinA,cosB∈(0,1),
可得f(sinA)>f(cosB).
故选:A.
点评 本题考查函数的周期性和对称性、奇偶性的判断和运用,考查单调性的运用,以及正弦函数的图象和性质,考查运算能力,属于中档题.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
16.已知双曲线的焦点分别为(0,-2)、(0,2),且经过点P(-3,2),则双曲线的标准方程是( )
| A. | $\frac{x^2}{3}-{y^2}$=1 | B. | $\frac{y^2}{3}-{x^2}$=1 | C. | y2-$\frac{x^2}{3}$=1 | D. | $\frac{x^2}{2}-\frac{y^2}{2}$=1 |
17.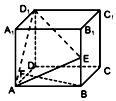 在如图所示的正四棱柱ABCD-A1B1C1D1中,E、F分别是棱B1B、AD的中点,直线BF与平面AD1E的位置关系是( )
在如图所示的正四棱柱ABCD-A1B1C1D1中,E、F分别是棱B1B、AD的中点,直线BF与平面AD1E的位置关系是( )
 在如图所示的正四棱柱ABCD-A1B1C1D1中,E、F分别是棱B1B、AD的中点,直线BF与平面AD1E的位置关系是( )
在如图所示的正四棱柱ABCD-A1B1C1D1中,E、F分别是棱B1B、AD的中点,直线BF与平面AD1E的位置关系是( )| A. | 平行 | B. | 相交但不垂直 | C. | 垂直 | D. | 异面 |
14.下列四个命题中是真命题的是( )
| A. | x>3是x>5的充分条件 | B. | x2=1是x=1的充分条件 | ||
| C. | a>b是ac2>bc2的必要条件 | D. | $α=\frac{π}{2}是sinα=1的必要条件$ |
15.下列函数中,在区间(0,+∞)上是增函数的是( )
| A. | y=-x2+1 | B. | y=x-2 | C. | y=log2x | D. | y=($\frac{1}{2}$)x |
16.已知函数$f(x)=|x|+{2^x}-\frac{1}{2}({x<0})$与g(x)=|x|+log2(x+a)的图象上存在关于y轴对称的点,则a的取值范围是( )
| A. | $({-∞,-\sqrt{2}})$ | B. | $({-∞,\sqrt{2}})$ | C. | $({-∞,2\sqrt{2}})$ | D. | $({-2\sqrt{2},\frac{{\sqrt{2}}}{2}})$ |