已知$f(x)=\left\{{\begin{array}{l}{{2^x}-2.x≥0}\\{-{x^2}+3.x＜0}\end{array}}\right.$.若fA．2B．-1或2C．±1或2D．1或2 题目和参考答案——青夏教育精英家教网—

题目内容

1．已知$f（x）=\left\{{\begin{array}{l}{{2^x}-2，x≥0}\\{-{x^2}+3，x＜0}\end{array}}\right.$，若f（a）=2，则a的取值为（　　）

A．

B．

-1或2

C．

±1或2

D．

1或2

分析利用分段函数通过x的范围，分别列出方程求出a即可．

解答解：$f（x）=\left\{{\begin{array}{l}{{2^x}-2，x≥0}\\{-{x^2}+3，x＜0}\end{array}}\right.$，若f（a）=2，当a≥0时，2^a-2=2，解得a=2．
当a＜0时，-a²+3=2，解得a=-1．
综上a的取值为：-1或2．
故选：B．

点评本题考查分段函数的应用，函数的零点的求法，考查计算能力．

练习册系列答案

成长记寒假总动员云南科技出版社系列答案

12．直线$ρcosθ=\frac{1}{2}$被圆ρ=1所截得的弦长为（　　）

9．在△ABC中，角A，B，C的对边分别是a、b、c，已知$\overrightarrow a=（{cosA，cosB}）$，$\overrightarrow b=（{a，2c-b}）$，且$\overrightarrow a∥\overrightarrow b$．
（Ⅰ）求角A的大小；
（Ⅱ）若b=3，△ABC的面积${S_{△ABC}}=3\sqrt{3}$，求a的值．

16．已知函数$f（x）=|x|+{2^x}-\frac{1}{2}（{x＜0}）$与g（x）=|x|+log₂（x+a）的图象上存在关于y轴对称的点，则a的取值范围是（　　）

$（{-2\sqrt{2}，\frac{{\sqrt{2}}}{2}}）$

6．已知函数$f（x）=2sin（{2x+\frac{π}{3}}）$的图象为C，则：①C关于直线$x=\frac{7}{12}π$对称；②C关于点$（{\frac{π}{12}，0}）$对称；③f（x）在$（{-\frac{π}{3}，\frac{π}{12}}）$上是增函数；④由y=2cos2x的图象向右平移$\frac{π}{12}$个单位长度可以得到图象C．以上结论正确的有（　　）

13．设函数f（x）=$\sqrt{3}sinxcosx+{sin^2}$x．
（1）当$x∈[{0，\frac{π}{2}}]$时，求f（x）的最大值；
（2）设A，B，C为△ABC的三个内角，$f（{\frac{C}{2}}）=1$，且C为锐角，c=$\sqrt{3}$，求a-b的取值范围．

10．已知曲线C₁的极坐标方程为ρ²cos2θ=8，曲线C₂的极坐标方程为$θ=\frac{π}{6}$，曲线C₁、C₂相交于A、B两点．
（Ⅰ）求A、B两点的极坐标；
（Ⅱ）曲线C₁与直线$\left\{\begin{array}{l}x=2+\frac{{\sqrt{3}}}{2}t\\ y=\frac{1}{2}t\end{array}\right.$（t为参数）分别相交于M，N两点，求线段MN的长度．

11．

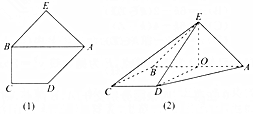如图（1），在五边形BCDAE中，CD∥AB，∠BCD=90°，CD=BC=1，AB=2，△ABE是以AB为斜边的等腰直角三角形，现将△ABE沿AB折起，使平面ABE⊥平面ABCD，如图（2），记线段AB的中点为O．
（Ⅰ）求证：平面ABE⊥平面EOD；
（Ⅱ）求平面ECD与平面ABE所成的锐二面角的大小．

试题分类