题目内容
8.若函数f(x)=$\frac{{a{x^2}}}{2}-({1+2a})x+2lnx({a>0})$在区间$({\frac{1}{2},1})$内有极大值,则a的取值范围是( )| A. | $({\frac{1}{e},+∞})$ | B. | (1,+∞) | C. | (1,2) | D. | (2,+∞) |
分析 求出函数的导数,问题转化为f′(x)在($\frac{1}{2}$,1)先大于0,再小于0,得到关于a的不等式组,解出即可.
解答 解:f′(x)=ax-(1+2a)+$\frac{2}{x}$=$\frac{{ax}^{2}-(2a+1)x+2}{x}$,(a>0,x>0)
若f(x)在($\frac{1}{2}$,1)有极大值,
则f′(x)在($\frac{1}{2}$,1)先大于0,再小于0,
则$\left\{\begin{array}{l}{f′(\frac{1}{2})>0}\\{f′(1)<0}\end{array}\right.$,解得:1<a<2,
故选:C.
点评 本题考查了函数的单调性、极值的意义,考查不等式以及二次函数的性质,是一道中档题.

练习册系列答案
相关题目
16.已知函数$f(x)=|x|+{2^x}-\frac{1}{2}({x<0})$与g(x)=|x|+log2(x+a)的图象上存在关于y轴对称的点,则a的取值范围是( )
| A. | $({-∞,-\sqrt{2}})$ | B. | $({-∞,\sqrt{2}})$ | C. | $({-∞,2\sqrt{2}})$ | D. | $({-2\sqrt{2},\frac{{\sqrt{2}}}{2}})$ |
3.运行如图所示的程序框图,若输出的y值为$-\sqrt{2}$,则判断框中应填写的条件是( )
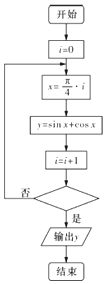

| A. | i>5? | B. | i>3? | C. | i>6? | D. | i>4? |
20.复数z满足zi=1-$\sqrt{5}$i(i为虚数单位),则z等于( )
| A. | -$\sqrt{5}$-i | B. | $\sqrt{5}$-i | C. | i | D. | -i |
17.若实数x、y满足$\left\{\begin{array}{l}{2x-y+2≥0}\\{2x+y-6≤0}\\{0≤y≤3}\end{array}\right.$,且z=3x-y,则z的最大值为( )
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | 9 | D. | -3 |
18.已知f(x)=sinx-x,命题p:?x∈(0,$\frac{π}{2}}$),f(x)<0,则( )
| A. | p是假命题,¬p::?x∈(0,$\frac{π}{2}}$),f(x)≥0 | B. | p是假命题,¬p::?x∈(0,$\frac{π}{2}}$),f(x)≥0 | ||
| C. | P是真命题,¬p::?x∈(0,$\frac{π}{2}}$),f(x)≥0 | D. | p是真命题,¬p::?x∈(0,$\frac{π}{2}}$),f(x)≥0 |