题目内容

7．已知动点P（x，y）满足5$\sqrt{{（x-1）}^{2}{+（y-2）}^{2}}$=|3x+4y-1|，则点P的轨迹是（　　）
A．直线B．抛物线C．双曲线D．椭圆

分析 利用方程转化动点的几何意义，然后求解判断轨迹即可．

解答 解：动点P（x，y）满足5$\sqrt{{（x-1）}^{2}{+（y-2）}^{2}}$=|3x+4y-1|，
可得：$\sqrt{{（x-1）}^{2}{+（y-2）}^{2}}$=$\frac{|3x+4y-1|}{5}$，表示动点P（x，y）到（1，2）与到直线3x+4y-1=0距离相等，
又（1，2）不在直线3x+4y-1=0上，则点P的轨迹是以（1，2）为焦点以直线3x+4y-1=0为准线的抛物线．
故选：B．

点评 本题考查轨迹方程的求法，轨迹的判断，注意抛物线的定义域本题直线方程的区别，是易错题．

练习册系列答案
相关题目
17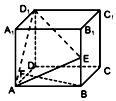．在如图所示的正四棱柱ABCD-A1B1C1D1中，E、F分别是棱B1B、AD的中点，直线BF与平面AD1E的位置关系是（　　）
A．平行B．相交但不垂直C．垂直D．异面
18．近来鸡蛋价格起伏较大，假设第一周、第二周鸡蛋价格分别为a元/斤、b元/斤，家庭主妇甲和乙买鸡蛋的方式不同：家庭主妇甲每周买3斤鸡蛋，家庭主妇乙每周买10元钱的鸡蛋，试比较谁的购买方式更优惠（两次平均价格低视为实惠）乙（在横线上填甲或乙即可）
15．下列函数中，在区间（0，+∞）上是增函数的是（　　）
A．y=-x2+1B．y=x-2C．y=log2xD．y=（$\frac{1}{2}$）x
2．已知集合A={x|y=lg（2-x）}，集合B=[y|y=$\sqrt{x}$}，则A∩B=[0，2）．
12．直线$ρcosθ=\frac{1}{2}$被圆ρ=1所截得的弦长为（　　）
A．1B．$\sqrt{3}$C．2D．4
19．某超市从现有甲、乙两种酸奶的日销售量（单位：箱）的1200个数据（数据均在区间（0，50]内）中，按照5%的比例进行分层抽样，统计结果按（0，10]，（10，20]，（20，30]，（30，40]，（40，50]分组，整理如下图：

（Ⅰ）写出频率分布直方图（图乙）中a的值；记所抽取样本中甲种酸奶与乙种酸奶日销售量的方差分别为$s_1^2$，$s_2^2$，试比较$s_1^2$与$s_2^2$的大小（只需写出结论）；
（Ⅱ）从甲种酸奶日销售量在区间（0，20]的数据样本中抽取3个，记在（0，10]内的数据个数为X，求X的分布列；
（Ⅲ）估计1200个日销售量数据中，数据在区间（0，10]中的个数．
16．已知函数$f（x）=|x|+{2^x}-\frac{1}{2}（{x＜0}）$与g（x）=|x|+log2（x+a）的图象上存在关于y轴对称的点，则a的取值范围是（　　）
A．$（{-∞，-\sqrt{2}}）$B．$（{-∞，\sqrt{2}}）$C．$（{-∞，2\sqrt{2}}）$D．$（{-2\sqrt{2}，\frac{{\sqrt{2}}}{2}}）$
17．若实数x、y满足$\left\{\begin{array}{l}{2x-y+2≥0}\\{2x+y-6≤0}\\{0≤y≤3}\end{array}\right.$，且z=3x-y，则z的最大值为（　　）
A．$\frac{3}{2}$B．-$\frac{3}{2}$C．9D．-3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网