题目内容
6．已知向量$\overrightarrow{a}$=（2，-1），$\overrightarrow{b}$=（x，3），当x为何值时：（1）$\overrightarrow{a}$∥$\overrightarrow{b}$；
（2）$\overrightarrow{a}$⊥$\overrightarrow{b}$；
（3）向量$\overrightarrow{a}$与向量$\overrightarrow{b}$的夹角是钝角．
分析 根据向量的共线定理和数量积运算公式列出方程或不等式解出．
解答 解：（1）∵$\overrightarrow{a}$∥$\overrightarrow{b}$，∴2×3+x=0，解得x=-6．
（2）∵$\overrightarrow{a}$⊥$\overrightarrow{b}$，∴2x-3=0，解得x=$\frac{3}{2}$．
（3）∵向量$\overrightarrow{a}$与向量$\overrightarrow{b}$的夹角是钝角，
∴$\overrightarrow{a}•\overrightarrow{b}＜$0，即2x-3＜0，解得x$＜\frac{3}{2}$．
当$\overrightarrow{a}，\overrightarrow{b}$方向相反时，$\overrightarrow{a}∥\overrightarrow{b}$，∴x=-6．
∴当向量$\overrightarrow{a}$与向量$\overrightarrow{b}$的夹角是钝角时，x＜$\frac{3}{2}$且x≠-6．
点评 本题考查了向量数量积运算，共线向量的坐标表示，属于基础题．
练习册系列答案
相关题目
16．
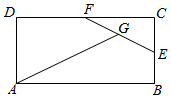如图，在矩形ABCD中，AB=2AD，E，F分别为BC，CD的中点，G为EF中点，
则$\overrightarrow{AG}$=（ ）
如图，在矩形ABCD中，AB=2AD，E，F分别为BC，CD的中点，G为EF中点，则$\overrightarrow{AG}$=（ ）
| A． | $\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AD}$ | B． | $\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$ | C． | $\frac{3}{4}\overrightarrow{AB}+\frac{3}{4}\overrightarrow{AD}$ | D． | $\frac{2}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$ |
17．已知集合A={x|x2+2x-3≥0}，B={x|-2≤x＜2}，则A∩B=（ ）
| A． | [-2，-1] | B． | [-1，2） | C． | [-2，1] | D． | [1，2） |
18．不等式组$\left\{\begin{array}{l}{x-y≤0}&{\;}\\{x+y≥-2}&{\;}\\{x-2y≥-2}&{\;}\end{array}\right.$的解集记为D，若（a，b）∈D，则z=2a-3b的最小值是（ ）
| A． | -4 | B． | -1 | C． | 1 | D． | 4 |
15．已知cos（$\frac{π}{12}$-θ）=$\frac{1}{3}$，则sin（$\frac{5π}{12}+θ$）的值是（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{2\sqrt{2}}{3}$ | C． | -$\frac{1}{3}$ | D． | -$\frac{2\sqrt{2}}{3}$ |