题目内容
2.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),点A,F分别是椭圆C的左顶点和左焦点,点P是⊙O:x2+y2=b2上的动点,若$\frac{|AP|}{|FP|}$是常数,则椭圆C的离心率为$\frac{\sqrt{5}-1}{2}$.分析 设F(-c,0),由c2=a2-b2可求c,P(x1,y1),要使得$\frac{|AP|}{|FP|}$是常数,则有(x1+a)2+y12=λ[(x1+c)2+y12]比较两边可得c,a的关系,结合椭圆的离心率公式,解方程可得可求.
解答 解:设F(-c,0),c2=a2-b2,A(-a,0),P(x1,y1),
使得$\frac{|AP|}{|FP|}$是常数,
设$\frac{|AP|}{|FP|}$=$\sqrt{λ}$,则有(x1+a)2+y12=λ[(c+x1)2+y12](x,λ是常数),
即b2+2ax1+a2=λ(b2+2cx1+c2),
比较两边,b2+a2=λ(b2+c2),a=λc,
故cb2+ca2=a(b2+c2),即ca2-c3+ca2=a3,
即e3-2e+1=0,
∴(e-1)(e2+e-1)=0,
∴e=1或e=$\frac{-1±\sqrt{5}}{2}$,
∵0<e<1,∴e=$\frac{\sqrt{5}-1}{2}$.
故答案为:$\frac{\sqrt{5}-1}{2}$.
点评 本题考查椭圆的简单性质,主要考查椭圆的离心率,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.在正方体ABCD-A1B1C1D1中,E、F分别为AB、C1D1的中点,则A1B1与平面A1EF夹角的正弦值为( )
| A. | $\frac{\sqrt{6}}{2}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{6}}{4}$ | D. | $\sqrt{2}$ |
11.抛物线y2=2x上与其焦点距离等于3的点的横坐标是( )
| A. | 1 | B. | 2 | C. | $\frac{5}{2}$ | D. | $\frac{7}{2}$ |
12.下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
(1)请根据上表提供的数据,用最小二乘法求出y关于x的回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{c}$;
(2)已知该厂技改前100吨甲产品的生产能耗为85吨标准煤.试根据(2)求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式:$\left\{\begin{array}{l}\hat b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}\\ \hat a=\overline y-\hat b\overline x\end{array}\right.$.
| x | 2 | 3 | 4 | 5 |
| y | 1.5 | 2 | 3 | 3.5 |
(2)已知该厂技改前100吨甲产品的生产能耗为85吨标准煤.试根据(2)求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式:$\left\{\begin{array}{l}\hat b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}\\ \hat a=\overline y-\hat b\overline x\end{array}\right.$.
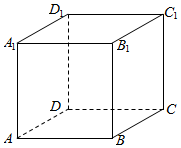 如图所示,在棱长为1的正方体ABCD-A1B1C1D1中.
如图所示,在棱长为1的正方体ABCD-A1B1C1D1中. 如图,椭圆的中心在原点,顶点分别是A1,A2,B1,B2,焦点分别为F1,F2,延长B1F2与A2B2交于点P,若∠B1PA2为钝角,则此椭圆的离心率的取值范围为($\frac{\sqrt{5}-1}{2}$,1).
如图,椭圆的中心在原点,顶点分别是A1,A2,B1,B2,焦点分别为F1,F2,延长B1F2与A2B2交于点P,若∠B1PA2为钝角,则此椭圆的离心率的取值范围为($\frac{\sqrt{5}-1}{2}$,1).