题目内容
如图是一个几何体的三视图,根据图中数据,可得该几何体的体积是( )

A、π+
| ||
B、π+2
| ||
C、2π+
| ||
D、2π+2
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:根据已知中的三视图可得该几何体是一个圆柱和三棱柱组成的组合体,分别求出圆柱和棱柱的体积,相加可得答案.
解答:
解:根据已知中的三视图可得该几何体是一个圆柱和三棱柱组成的组合体,
其中棱柱的体积为:
×
×
×
=
,
圆柱的体积为:π×(
)2×2=2π,
故该组合体的体积V=2π+
,
故选:C
其中棱柱的体积为:
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
圆柱的体积为:π×(
| 2 |
| 2 |
故该组合体的体积V=2π+
| 2 |
故选:C
点评:本题考查三视图复原几何体形状的判断,几何体的表面积与体积的求法,考查空间想象能力与计算能力.

练习册系列答案
相关题目
 运行如图所示的程序框图,输出A,B,C的一组数据为
运行如图所示的程序框图,输出A,B,C的一组数据为 | 3 |
| A、垂直、相切 |
| B、平行、相交 |
| C、垂直、相离 |
| D、平行、相切 |
若ax(1+
)5的展开式中x2项的系数是20,则实数a等于( )
| x |
| A、2 | B、3 | C、4 | D、5 |
在△ABC中,若对任意的λ∈R,都有|
+λ
|≥|
|,则△ABC( )
| AB |
| AC |
| BC |
| A、一定为锐角三角形 |
| B、一定为钝角三角形 |
| C、一定为直角三角形 |
| D、可以为任意三角形 |
已知an=
,则这个数列的前30项中最大项和最小项分别是( )
n-
| ||
n-
|
| A、a1,a30 |
| B、a1,a9 |
| C、a10,a30 |
| D、a10,a9 |
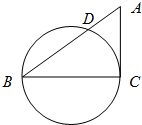
已知Rt△ABC中,∠C=90°,AB=5,BC=4,以BC为直径的圆交AB于D,则BD的长为( )

| A、4 | ||
B、
| ||
C、
| ||
D、
|
已知三棱柱ABC-A1B1C1侧棱与底面垂直,且其六个顶点都在球O的球面上,若AC=3,AB=4,CB=5,球O的半径为6,则OA与平面ABC所成的角的余弦值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|