题目内容
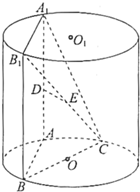 如图,AA1、BB1为圆柱OO1的母线(母线与底面垂直),BC是底面圆O的直径,D、E分别是AA1、CB1的中点,DE⊥平面CBB1.
如图,AA1、BB1为圆柱OO1的母线(母线与底面垂直),BC是底面圆O的直径,D、E分别是AA1、CB1的中点,DE⊥平面CBB1.(1)证明:AC⊥平面AA1B1B;
(2)证明:DE∥平面ABC;
(3)求四棱锥C-ABB1A1与圆柱OO1的体积比.
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)由已知条件推导出CA⊥AB,AA1⊥平面ABC,由此能证明CA⊥平面AA1B1B.
(2)连接EO、OA,得到EO∥BB1,且EO=
BB1 ,由此能求出四边形AOED是平行四边形,由此能证明DE∥平面ABC.
(3)连接CA.由题知DE⊥平面CBB1,由DE∥OA,知CA为四棱锥C-ABB1A1的高,由此能求出四棱锥C-ABB1A1与圆柱OO1的体积比.
(2)连接EO、OA,得到EO∥BB1,且EO=
| 1 |
| 2 |
(3)连接CA.由题知DE⊥平面CBB1,由DE∥OA,知CA为四棱锥C-ABB1A1的高,由此能求出四棱锥C-ABB1A1与圆柱OO1的体积比.
解答:
 (1)证明:∵BC是底面圆O的直径,∴CA⊥AB.
(1)证明:∵BC是底面圆O的直径,∴CA⊥AB.
又AA1是圆柱的母线,∴AA1⊥平面ABC,
∴AA1⊥CA,又AA1∩AB=A,
∴CA⊥平面AA1B1B.…(4分)
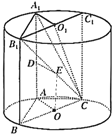
(2)如图,连接EO、OA,∵E,O分别为CB1、BC的中点,
∴EO是△BB1C的中位线,∴EO∥BB1,且EO=
BB1 .
又DA∥BB1,AA1=BB1,
故DA=
BB1=EO,∴DA∥EO,且DA=EO,
∴四边形AOED是平行四边形,即DE∥OA,
又DE不包含平面ABC,OA?平面ABC,
∴DE∥平面ABC.…(8分)
(3)如图,连接CA.由题知DE⊥平面CBB1,
且由(2)知DE∥OA,
∴AO⊥平面CBB1,∴AO⊥BC,
∴AC=AB=
OA.
由(1)知CA为四棱锥C-ABB1A1的高.
设圆柱高为h,底面半径为r,
则V圆柱=πr2h,VC-ABB1A1=
h(
r)•(
r)=
hr2,
∴VC-ABB1A1:V圆柱=
=
.…(12分)
 (1)证明:∵BC是底面圆O的直径,∴CA⊥AB.
(1)证明:∵BC是底面圆O的直径,∴CA⊥AB.又AA1是圆柱的母线,∴AA1⊥平面ABC,
∴AA1⊥CA,又AA1∩AB=A,
∴CA⊥平面AA1B1B.…(4分)
(2)如图,连接EO、OA,∵E,O分别为CB1、BC的中点,
∴EO是△BB1C的中位线,∴EO∥BB1,且EO=
| 1 |
| 2 |
又DA∥BB1,AA1=BB1,
故DA=
| 1 |
| 2 |
∴四边形AOED是平行四边形,即DE∥OA,
又DE不包含平面ABC,OA?平面ABC,
∴DE∥平面ABC.…(8分)
(3)如图,连接CA.由题知DE⊥平面CBB1,
且由(2)知DE∥OA,
∴AO⊥平面CBB1,∴AO⊥BC,
∴AC=AB=
| 2 |
由(1)知CA为四棱锥C-ABB1A1的高.
设圆柱高为h,底面半径为r,
则V圆柱=πr2h,VC-ABB1A1=
| 1 |
| 3 |
| 2 |
| 2 |
| 2 |
| 3 |
∴VC-ABB1A1:V圆柱=
| ||
| πr2h |
| 2 |
| 3π |
点评:本题考查直线与平面垂直的证明,考查直线与平面平行的证明,考查棱锥与圆柱体积的比的求法,解题时要注意空间思维能力的培养.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
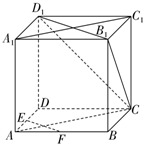 如图,在正方体ABCD-A1B1C1D1中,E、F分别为棱AD、AB的中点.求证:EF∥平面CB1D1.
如图,在正方体ABCD-A1B1C1D1中,E、F分别为棱AD、AB的中点.求证:EF∥平面CB1D1. 如图所示,以等腰直角三角形ABC斜边BC上的高AD为折痕.使△ABD和△ACD折成互相垂直的两个平面,则∠BAC=
如图所示,以等腰直角三角形ABC斜边BC上的高AD为折痕.使△ABD和△ACD折成互相垂直的两个平面,则∠BAC=