题目内容
已知函数f(x)满足f(
)=
(1)求f(x)的解析式及定义域;
(2)求f(x)的值域.
| 1-x |
| 1+x |
| 1-x2 |
| 1+x2 |
(1)求f(x)的解析式及定义域;
(2)求f(x)的值域.
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)用换元法,设
=t,求出x,得出f(t),即为f(x)的解析式;
(2)分x>0,x=0,x<0时,求出
的取值范围,即是函数f(x)的值域.
| 1-x |
| 1+x |
(2)分x>0,x=0,x<0时,求出
| 2x |
| 1+x2 |
解答:
解:(1)根据题意,设
=t,
则x=
(t≠-1);
∴f(t)=
=
(t≠-1);
即f(x)=
,定义域是{x|x≠-1};
(2)当x>0时,0<2x≤1+x2,∴0<
≤1;
当x=0时,
=0;
当x<0时,0<-2x≤1+x2,∴0<
≤1,
∴-1≤
≤0;
又∵x≠-1,∴
≠-1;
综上,-1<
≤1;
即f(x)∈(-1,1].
| 1-x |
| 1+x |
则x=
| 1-t |
| 1+t |
∴f(t)=
1-(
| ||
1+(
|
=
| 2t |
| 1+t2 |
即f(x)=
| 2x |
| 1+x2 |
(2)当x>0时,0<2x≤1+x2,∴0<
| 2x |
| 1+x2 |
当x=0时,
| 2x |
| 1+x2 |
当x<0时,0<-2x≤1+x2,∴0<
| -2x |
| 1+x2 |
∴-1≤
| 2x |
| 1+x2 |
又∵x≠-1,∴
| 2x |
| 1+x2 |
综上,-1<
| 2x |
| 1+x2 |
即f(x)∈(-1,1].
点评:本题考查了函数的定义域和值域的问题,解题时应用换元法求出函数的解析式,根据解析式求出定义域和值域,是基础题.

练习册系列答案
相关题目
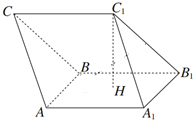 如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2
如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2 如图,在Rt△ABC中,AB=BC,以AB为直径的⊙O交AC于D,过D作DE⊥BC,垂足为E,连接AE交⊙O于点F,求证:CE2=EF•EA.
如图,在Rt△ABC中,AB=BC,以AB为直径的⊙O交AC于D,过D作DE⊥BC,垂足为E,连接AE交⊙O于点F,求证:CE2=EF•EA.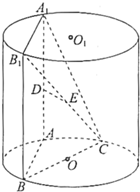 如图,AA1、BB1为圆柱OO1的母线(母线与底面垂直),BC是底面圆O的直径,D、E分别是AA1、CB1的中点,DE⊥平面CBB1.
如图,AA1、BB1为圆柱OO1的母线(母线与底面垂直),BC是底面圆O的直径,D、E分别是AA1、CB1的中点,DE⊥平面CBB1.