题目内容
下列命题中正确的有
(1)若不等式(m+n)(
+
)≥25对任意正实数m,n恒成立,则正实数a的最小值为16.
(2)命题“?x>1,2x-a>0”的否定为“?x>1,2x-a<0”
(3)在一个2×2列联表中,计算得K2=13,则有99%的把握确定这两个变量间有关系.
(4)函数f(x)=sinx-x的零点个数有三个.
临界值表:
(1)若不等式(m+n)(
| a |
| m |
| 1 |
| n |
(2)命题“?x>1,2x-a>0”的否定为“?x>1,2x-a<0”
(3)在一个2×2列联表中,计算得K2=13,则有99%的把握确定这两个变量间有关系.
(4)函数f(x)=sinx-x的零点个数有三个.
临界值表:
| P(k2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
考点:独立性检验的基本思想,特称命题
专题:阅读型,概率与统计
分析:(1)根据均值不等式成立的条件可判断(1)是否正确;
(2)根据全称命题的否定是特称命题,写出其否定命题,判断(2)是否正确;
(3)比较相关指数的观测值与临界值的大小,可得两个变量有关系的可靠性程度,由此可判断(3)的正确性;
(4)根据正弦线的性质,可得x>0时,x>sinx,根据函数是奇函数,函数f(x)=sinx-x只有一个零点x=0,由此可判断(4)是否正确.
(2)根据全称命题的否定是特称命题,写出其否定命题,判断(2)是否正确;
(3)比较相关指数的观测值与临界值的大小,可得两个变量有关系的可靠性程度,由此可判断(3)的正确性;
(4)根据正弦线的性质,可得x>0时,x>sinx,根据函数是奇函数,函数f(x)=sinx-x只有一个零点x=0,由此可判断(4)是否正确.
解答:
解:(1)不等式(m+n)(
+
)=a+1+
+
≥a+1+2
≥25对任意正实数m,n恒成立,
又a为正实数,∴
+1≥5,∴a≥16,故(1)正确;
(2)命题“?x>1,2x-a>0”的否定为“?x≤1,2x-a≤0”,故(2)错误;
(3)∵计算得相关指数K2=13,则有99%以上的把握认为这两个变量间有关,故(3)正确;
(4)∵x>0时,x>sinx,∴函数f(x)=sinx-x只有一个零点x=0,故(4)错误.
故答案为:(1)、(3).
| a |
| m |
| 1 |
| n |
| na |
| m |
| m |
| n |
| a |
又a为正实数,∴
| a |
(2)命题“?x>1,2x-a>0”的否定为“?x≤1,2x-a≤0”,故(2)错误;
(3)∵计算得相关指数K2=13,则有99%以上的把握认为这两个变量间有关,故(3)正确;
(4)∵x>0时,x>sinx,∴函数f(x)=sinx-x只有一个零点x=0,故(4)错误.
故答案为:(1)、(3).
点评:本题考查了全称命题的否定,独立性检验基本思想及均值不等式的应用,熟练掌握均值不等式成立的条件是解题的关键.考查知识面广,解答要细心,熟练掌握均值不等式成立的条件是解题的关键.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
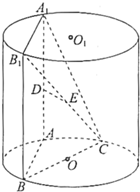 如图,AA1、BB1为圆柱OO1的母线(母线与底面垂直),BC是底面圆O的直径,D、E分别是AA1、CB1的中点,DE⊥平面CBB1.
如图,AA1、BB1为圆柱OO1的母线(母线与底面垂直),BC是底面圆O的直径,D、E分别是AA1、CB1的中点,DE⊥平面CBB1.