题目内容
数列{an}满足关系anan+1=1-an+1(n∈N*),且a2014=2,则a2012= .
考点:数列的函数特性
专题:等差数列与等比数列
分析:利用递推思想解题.
解答:
解:∵数列{an}满足关系anan+1=1-an+1(n∈N*),且a2014=2,
∴a2013•2=1-2,
解得a2013=-
,
∴a2012•(-
)=1-(-
)=
,
∴a2012=-3.
故答案为:-3.
∴a2013•2=1-2,
解得a2013=-
| 1 |
| 2 |
∴a2012•(-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴a2012=-3.
故答案为:-3.
点评:本题考查数列的第2012项的求法,是基础题,解题时要注意递推思想的合理运用.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
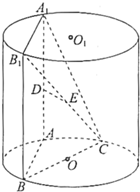 如图,AA1、BB1为圆柱OO1的母线(母线与底面垂直),BC是底面圆O的直径,D、E分别是AA1、CB1的中点,DE⊥平面CBB1.
如图,AA1、BB1为圆柱OO1的母线(母线与底面垂直),BC是底面圆O的直径,D、E分别是AA1、CB1的中点,DE⊥平面CBB1.