题目内容
数列{an}中,a1=8,a4=2,且满足:an+2-2an+1+an=0(n∈N*),
(1)求数列{an}的通项公式;
(2)设bn=
(n∈N*),求证:Sn=b1+b2+…+bn<
.
(1)求数列{an}的通项公式;
(2)设bn=
| 1 |
| n(12-an) |
| 1 |
| 2 |
考点:数列的求和,数列与不等式的综合
专题:等差数列与等比数列
分析:(1)由已知得an+2-an+1=an+1-an(n∈N*),由此能求出an=10-2n.
(2)由bn=
=
=
(
-
),利用裂项求和法能证明Sn=b1+b2+…+bn<
.
(2)由bn=
| 1 |
| n(12-an) |
| 1 |
| n(12-10+2n) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 2 |
解答:
(1)解:∵an+2-2an+1+an=0,
∴an+2-an+1=an+1-an(n∈N*)
∴{an}是等差数列,设公差为d,
∵a1=8,a4=a1+3d=8+3d=2,∴d=-2,
∴an=8+(n-1)(-2)=10-2n.
(2)证明:bn=
=
=
=
(
-
),
∴Sn=b1+b2+…+bn
=
[(1-
)+(
-
)+…+(
-
)]
=
(1-
)<
,
∴Sn=b1+b2+…+bn<
.
∴an+2-an+1=an+1-an(n∈N*)
∴{an}是等差数列,设公差为d,
∵a1=8,a4=a1+3d=8+3d=2,∴d=-2,
∴an=8+(n-1)(-2)=10-2n.
(2)证明:bn=
| 1 |
| n(12-an) |
| 1 |
| n(12-10+2n) |
=
| 1 |
| 2n(n+1) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+1 |
∴Sn=b1+b2+…+bn
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| 2 |
∴Sn=b1+b2+…+bn<
| 1 |
| 2 |
点评:本题考查数列的通项公式的求法,考查不等式的证明,解题时要认真审题,注意裂项法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在试验中随机事件A的频率p=
满足( )
| nA |
| n |
| A、0<P≤1 |
| B、0≤p<1 |
| C、0<p<1 |
| D、0≤p≤1 |
曲线y=x3-2x2-4x+2在点(1,-3)处的切线方程是( )
| A、5x+y+2=0 |
| B、5x+y-2=0 |
| C、5x-y-8=0 |
| D、5x-y+8=0 |
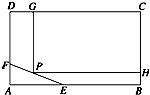 如图,长方形ABCD形状的空地,AB=100m,BC=80m,现决定在该空地上规划出一块矩形CGPH地面学生公寓,要求一边落在CD 上,但不得越过文物保护区△AEF的EF.△AEF的边AE=30m,AF=20m.
如图,长方形ABCD形状的空地,AB=100m,BC=80m,现决定在该空地上规划出一块矩形CGPH地面学生公寓,要求一边落在CD 上,但不得越过文物保护区△AEF的EF.△AEF的边AE=30m,AF=20m.