题目内容
19.已知α是第二象限角,且cos(α+π)=$\frac{3}{13}$.(1)求tanα的值;
(2)求sin(α-$\frac{π}{2}$)•sin(-α-π)的值.
分析 (1)利用诱导公式可求cosα,利用同角三角函数基本关系式可求sinα,tanα的值.
(2)利用诱导公式化简所求即可计算得解.
解答 (本小题满分为10分)
解:(1)∵cos(α+π)=$\frac{3}{13}$=-cosα,可得:cosα=-$\frac{3}{13}$,
又∵α是第二象限角,
∴sinα=$\sqrt{1-co{s}^{2}α}$=$\frac{4\sqrt{10}}{13}$,tanα=$\frac{sinα}{cosα}$=-$\frac{4\sqrt{10}}{3}$.
(2)sin(α-$\frac{π}{2}$)•sin(-α-π)=(-cosα)•sinα=(-$\frac{3}{13}$)×$\frac{4\sqrt{10}}{13}$=-$\frac{12\sqrt{10}}{169}$.
点评 本题主要考查了诱导公式,同角三角函数基本关系式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.集合A={0,2,4,6},B={x||x-1|≤2},则A∩B是( )
| A. | {0,2} | B. | {2,4} | C. | {4,6} | D. | {0,2,4} |
4.在空间直角坐标中,点P(-1,-2,-3)到平面xOz的距离是( )
| A. | 1 | B. | 2 | C. | 3 | D. | $\sqrt{14}$ |
11.已知条件p:x>1,条件q:x>0,则p是q的( )条件.
| A. | 充要 | B. | 充分不必要 | ||
| C. | 必要不充分 | D. | 既非充分也非必要 |
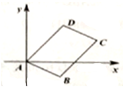 如图,面积为8的平行四边形ABCD,A为坐标原点,B坐标为(2,-1),C、D均在第一象限.
如图,面积为8的平行四边形ABCD,A为坐标原点,B坐标为(2,-1),C、D均在第一象限.