题目内容
20.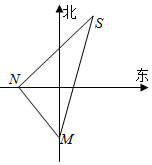 如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20n mile,随后货轮按北偏西30°的方向航行30min后,又测得灯塔在货轮的东北方向,则货轮的速度为( )
如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20n mile,随后货轮按北偏西30°的方向航行30min后,又测得灯塔在货轮的东北方向,则货轮的速度为( )| A. | 20($\sqrt{2}$+$\sqrt{6}$)n mile/h | B. | 20($\sqrt{6}$-$\sqrt{2}$)n mile/h | C. | 20($\sqrt{3}$+$\sqrt{6}$)n mile/h | D. | 20($\sqrt{6}$-$\sqrt{3}$)n mile/h |
分析 由题意知SM=20,∠SNM=105°,∠NMS=45°,∠MSN=30°,△MNS中利用正弦定理可得$\frac{MN}{sin30°}$=$\frac{20}{sin105°}$,代入可求MN,进一步利用速度公式即可.
解答 解:由题意知SM=20,∠NMS=45°,
∴SM与正东方向的夹角为75°,MN与正东方向的夹角为,60°
∴SNM=105°
∴∠MSN=30°,
△MNS中利用正弦定理可得,$\frac{MN}{sin30°}$=$\frac{20}{sin105°}$.
MN=$\frac{20×\frac{1}{2}}{\frac{\sqrt{2}+\sqrt{6}}{4}}$=10($\sqrt{6}-\sqrt{2}$)n mile,
∴货轮航行的速度v=$\frac{10(\sqrt{6}-\sqrt{2})}{\frac{1}{2}}$=20($\sqrt{6}-\sqrt{2}$) n mile/h.
故选:B.
点评 此题考查了正弦定理在解三角形中的应用,解决实际问题的关键是要把实际问题转化为数学问题,然后利用数学知识进行求解.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
10.已知i是虚数单位,复数z=(a+i)(1-i),若z的实部与虚部相等,则实数a=( )
| A. | 1 | B. | 0 | C. | -1 | D. | -2 |
11.《张丘建算经》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有女不善织,日减功迟,初日织五尺,末日织一尺,今三十织迄,问织几何.”其意思为:有个女子不善于织布,每天比前一天少织同样多的布,第一天织五尺,最后一天织一尺,三十天织完,问三十天共织布( )
| A. | 30尺 | B. | 90尺 | C. | 150尺 | D. | 180尺 |
8.已知函数f(x)=x3-x2-x+a的图象与x轴只有一个交点,则实数a的取值范围是( )
| A. | (-∞,-1)∪(-$\frac{1}{9}$,+∞) | B. | (-$\frac{5}{27}$,1) | C. | (-∞,1) | D. | (-∞,-$\frac{5}{27}$)∪(1,+∞) |
5.已知函数f(x)=cos2x+asinx在区间(0,nπ)内恰有8个零点,则实数a的取值范围与最小正整数n的值分别为( )
| A. | (-1,1),2 | B. | (-1,1),4 | C. | [-1,1],2 | D. | [-1,1],4 |
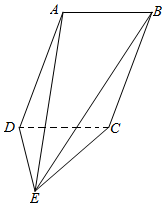 如图,平行四边形ABCD⊥平面CDE,AD=DC=DE=4,∠ADC=60°,AD⊥DE
如图,平行四边形ABCD⊥平面CDE,AD=DC=DE=4,∠ADC=60°,AD⊥DE