题目内容
12.已知点P在函数y=$\frac{1}{x}$的图象上,过点P的直线交x、y轴正半轴于点A、B,O为坐标原点,三角形△AOB的面积为S,若$\overrightarrow{BP}=λ\overrightarrow{PA}$且S∈[2,3],则λ的取值范围是[2-$\sqrt{3}$,2$+\sqrt{3}$].分析 设点A、B的坐标分别为(a,0),(0,b),P(x0,y0),a>0,b>0,由$\overrightarrow{BP}=λ\overrightarrow{PA}$,得到x0=$\frac{aλ}{1+λ}$,y0=-$\frac{b}{1+λ}$,根据函数的性质和三角形的面积公式即可表示出4≤$\frac{(1+λ)^{2}}{λ}$≤6,解得即可.
解答 解:设点A、B的坐标分别为(a,0),(0,b),P(x0,y0),a>0,b>0,
则由$\overrightarrow{BP}=λ\overrightarrow{PA}$,
∴x0=$\frac{aλ}{1+λ}$,y0=-$\frac{b}{1+λ}$,
∴x0•y0=$\frac{abλ}{(1+λ)^{2}}$=1,
∴ab=$\frac{(1+λ)^{2}}{λ}$,
∵S∈[2,3],S=$\frac{1}{2}$ab,
∴ab∈[4,6],
∴4≤$\frac{(1+λ)^{2}}{λ}$≤6,
解得.2-$\sqrt{3}$≤λ≤2$+\sqrt{3}$
故答案为:[2-$\sqrt{3}$,2$+\sqrt{3}$].
点评 本题考查了定比分点以及函数的性质和三角形的面积公式,属于中档题.

练习册系列答案
相关题目
2.在空间,下列说法正确的是( )
| A. | 两组对边相等的四边形是平行四边形 | |
| B. | 四边相等的四边形是菱形 | |
| C. | 平行于同一直线的两条直线平行 | |
| D. | 三点确定一个平面 |
3.已知椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$的右焦点为F,P是椭圆上一点,点$A({0,2\sqrt{3}})$,当△APF的周长最大时,△APF的面积等于( )
| A. | $\frac{{11\sqrt{3}}}{4}$ | B. | $\frac{{21\sqrt{3}}}{4}$ | C. | $\frac{11}{4}$ | D. | $\frac{21}{4}$ |
20.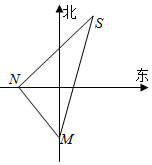 如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20n mile,随后货轮按北偏西30°的方向航行30min后,又测得灯塔在货轮的东北方向,则货轮的速度为( )
如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20n mile,随后货轮按北偏西30°的方向航行30min后,又测得灯塔在货轮的东北方向,则货轮的速度为( )
 如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20n mile,随后货轮按北偏西30°的方向航行30min后,又测得灯塔在货轮的东北方向,则货轮的速度为( )
如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20n mile,随后货轮按北偏西30°的方向航行30min后,又测得灯塔在货轮的东北方向,则货轮的速度为( )| A. | 20($\sqrt{2}$+$\sqrt{6}$)n mile/h | B. | 20($\sqrt{6}$-$\sqrt{2}$)n mile/h | C. | 20($\sqrt{3}$+$\sqrt{6}$)n mile/h | D. | 20($\sqrt{6}$-$\sqrt{3}$)n mile/h |