题目内容
如图为一个几何体的三视图,则该几何体的外接球的表面积为( )
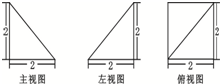

| A、4π | B、8π |
| C、12π | D、16π |
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:如图所示,该几何体为四棱锥P-ABCD,其中PA⊥底面ABCD,底面ABCD是边长为2的正方形,PA=2.取PC的中点O,则点O是该几何体的外接球的球心.求出即可.
解答:
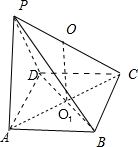 解:如图所示,该几何体为四棱锥P-ABCD,其中PA⊥底面ABCD,底面ABCD是边长为2的正方形,PA=2.
解:如图所示,该几何体为四棱锥P-ABCD,其中PA⊥底面ABCD,底面ABCD是边长为2的正方形,PA=2.
取PC的中点O,则点O是该几何体的外接球的球心.
OC=
PC=
=
.
∴该几何体的外接球的表面积=4πR2=12π.
故选:C.
 解:如图所示,该几何体为四棱锥P-ABCD,其中PA⊥底面ABCD,底面ABCD是边长为2的正方形,PA=2.
解:如图所示,该几何体为四棱锥P-ABCD,其中PA⊥底面ABCD,底面ABCD是边长为2的正方形,PA=2.取PC的中点O,则点O是该几何体的外接球的球心.
OC=
| 1 |
| 2 |
| 1 |
| 2 |
| PA2+AC2 |
| 3 |
∴该几何体的外接球的表面积=4πR2=12π.
故选:C.
点评:本题考查了四棱锥外接球的表面积、三视图的有关知识,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
某三棱锥的三视图如图所示,这个三棱锥最长棱的棱长是( )


| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
若函数f(x)=x2-2x(x∈R),则f(x)的零点个数为( )个.
| A、1 | B、2 | C、3 | D、4 |
△ABC的内角A,B,C的对边分别为a,b,c,若a,b,c成等比数列,且c=2a,则sinB=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中,M是BC的中点,AM=5,BC=6,则
•
等于( )
| AB |
| AC |
| A、9 | B、12 | C、16 | D、30 |
在R上定义的函数f(x)是偶函数,且f(x)=f(2-x),若f(x)在区间x∈[1,2)是减函数,则函数 f(x)( )
| A、在区间[-2,-1]上是减函数,区间[3,4]上是增函数 |
| B、在区间[-2,-1]上是减函数,区间[3,4]上是减函数 |
| C、在区间[-2,-1]上是增函数,区间[3,4]上是增函数 |
| D、在区间[-2,-1]上是增函数,区间[3,4]上是减函数 |
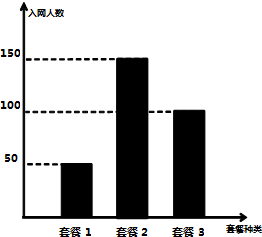 移动公司在国庆期间推出4G套餐,对国庆节当日办理套餐的客户进行优惠,优惠方案如下:选择套餐一的客户可获得优惠200元,选择套餐二的客户可获得优惠500元,选择套餐三的客户可获得优惠300元.国庆节当天参与活动的人数统计结果如图所示,现将频率视为概率.
移动公司在国庆期间推出4G套餐,对国庆节当日办理套餐的客户进行优惠,优惠方案如下:选择套餐一的客户可获得优惠200元,选择套餐二的客户可获得优惠500元,选择套餐三的客户可获得优惠300元.国庆节当天参与活动的人数统计结果如图所示,现将频率视为概率.