��Ŀ����
�����������⣺
��1���ڡ�ABC�У���A����B��cos2A��cos2B�ij�Ҫ������
��2���ˣ���Ϊʵ��������
=��
����
��
���ߣ�
��3��������
��
����|
|=|
|����
=
��
=-
��
��4������y=sin(2x+
)sin(
-2x)����С�������ǦУ�
��5��������p��
��0����?p��
��0
��6����a1=1��an=3n-1�����S1��S2��S3��������е�ǰn���Sn�ı���ʽ�������ǹ���������
������ȷ������ĸ���Ϊ��������
��1���ڡ�ABC�У���A����B��cos2A��cos2B�ij�Ҫ������
��2���ˣ���Ϊʵ��������
| a |
| b |
| a |
| b |
��3��������
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
��4������y=sin(2x+
| �� |
| 3 |
| �� |
| 6 |
��5��������p��
| 1 |
| x-1 |
| 1 |
| x-1 |
��6����a1=1��an=3n-1�����S1��S2��S3��������е�ǰn���Sn�ı���ʽ�������ǹ���������
������ȷ������ĸ���Ϊ��������
| A��1 | B��2 | C��3 | D��4 |
���㣺���������ж���Ӧ��
ר�⣺������
�������ɡ�A����B��sinA��sinB��Ȼ����ͬ�����Ǻ����Ļ�����ϵʽ�жϣ�1����������˵����2����3������
�������Ǻ������յ���ʽ�������ǵ����һ�����������˵����4����������p�ȼ�ת����˵����5������ֱ�ӹ��������Ķ���˵����6����ȷ��
�������Ǻ������յ���ʽ�������ǵ����һ�����������˵����4����������p�ȼ�ת����˵����5������ֱ�ӹ��������Ķ���˵����6����ȷ��
���
�⣺���ڣ�1�����ڡ�ABC�У���A����B����sinA��sinB����sin2A��sin2B��1-2sin2A��1-2sin2B��
��cos2A��cos2B����֮���������A����B��cos2A��cos2B�ij�Ҫ���������⣨1����ȷ��
���ڣ�2�����ˣ���Ϊʵ��������
=��
����
��
���ߴ�����=��=0ʱ��
��
�����ߣ����Ц�
=��
��
���ڣ�3����������
��
����|
|=|
|����
=
��
=-
���������������ڱ߹��ɵ���������|
|=|
|����
��
��
��-
��
���ڣ�4��������y=sin(2x+
)sin(
-2x)=
��2sin(2x+
)cos(2x+
)=
sin(4x+
)��������������
�����⣨4������
���ڣ�5����������pΪ��
��0����?p��
��0����ԭ����
��0�õ�x��1�������x��1����
��0����x=1��
���ڣ�6������a1=1��an=3n-1�����S1��S2��S3��������е�ǰn���Sn�ı���ʽ�������ǹ�����������ȷ��
��ѡ��B��
��cos2A��cos2B����֮���������A����B��cos2A��cos2B�ij�Ҫ���������⣨1����ȷ��
���ڣ�2�����ˣ���Ϊʵ��������
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
���ڣ�3����������
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
���ڣ�4��������y=sin(2x+
| �� |
| 3 |
| �� |
| 6 |
| 1 |
| 2 |
| �� |
| 3 |
| �� |
| 3 |
| 1 |
| 2 |
| 2�� |
| 3 |
| �� |
| 2 |
���ڣ�5����������pΪ��
| 1 |
| x-1 |
| 1 |
| x-1 |
| 1 |
| x-1 |
| 1 |
| x-1 |
���ڣ�6������a1=1��an=3n-1�����S1��S2��S3��������е�ǰn���Sn�ı���ʽ�������ǹ�����������ȷ��
��ѡ��B��
���������⿼�������������ж���Ӧ�ã�������ƽ���������ߵ����������������Ǻ������ڵ������е��⣮

��ϰ��ϵ�д�
 ��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д�
�����Ŀ
��֪������C��y2=8x�Ľ���ΪF����Ϊl��P��l��һ�㣬Q��ֱ��PF��C��һ�����㣬��
=4
����|QF|=��������
| PF |
| FQ |
A��
| ||
| B��5 | ||
C��
| ||
| D��2 |
��֪һ�������������ͼ��������ͼ��ʾ����ü����������ǣ�������


A��
| ||||
B��
| ||||
C��
| ||||
| D��1 |
��ͼΪһ�������������ͼ����ü�����������ı����Ϊ��������
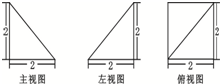

| A��4�� | B��8�� |
| C��12�� | D��16�� |
��֪����
=��1��2����
=��1+m��m-1������
��
����ʵ��m��ֵΪ��������
| a |
| b |
| a |
| b |
| A��3 | B��-3 | C��2 | D��-2 |