题目内容

△ABC的内角A，B，C的对边分别为a，b，c，若a，b，c成等比数列，且c=2a，则sinB=（　　）
A、
1
4
B、
3
4
C、
7
4
D、
2
3
考点：正弦定理
专题：解三角形
分析：直接利用等比数列求出abc的关系，结合已知条件利用余弦定理求出B的余弦函数值，然后求解sinB．
解答： 解：△ABC中，由a、b、c成等比数列，所以b2=ac，
由余弦定理可知：b2=a2+c2-2accosB，又c=2a，
∴2a2=a2+4a2-4a2cosB，
∴cosB=
3
4
，∴sinB=
1-cos2B
=
7
4
，
故选：C．
点评：本题主要考查余弦定理的应用，等比数列的定义，同角三角函数的基本关系，考查计算能力，属于基础题．
练习册系列答案
相关题目
已知抛物线C：y2=8x的焦点为F，准线为l，P是l上一点，Q是直线PF与C的一个交点，若
PF
=4
FQ
，则|QF|=（　　）
A、
7
2
B、5
C、
5
2
D、2
①如果一个几何体的三视图是完全相同的，则这个几何体一定是正方体；
②如果一个几何体的正视图和俯视图都是矩形，则这个几何体一定长方体；
③如果一个几何体的三视图都是矩形，则这个几何体是长方体；
④如果一个几何体的正视图和俯视图都是等腰梯形，则这个几何体一定圆台；
其中说法正确的是
 
．
如图为一个几何体的三视图，则该几何体的外接球的表面积为（　　）
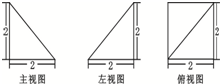
A、4πB、8π
C、12πD、16π
已知函数f（x）=
4x-4，x≤1
x2-4x+3，x＞1
，g（x）=lnx，则函数y=f（x）-g（x）的零点个数为（　　）
A、1B、2C、3D、4
若函数f（x）=e -(x-μ)2（e为无理数，e≈2.71828…）的最大值是m，且f（x）是偶函数，则m+μ=
 
．
设椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为e=
3
2
，M是椭圆C上的一点，且点M到椭圆C两焦点的距离之和为4．
（1）求椭圆C的方程；
（2）过椭圆C的左顶点A的直线l交椭圆于另一点B，P（0，t）是y轴上一点，满足|PA|=|PB|，
PA
•
PB
=4，求实数t的值．
已知向量
a
=（1，2），
b
=（1+m，m-1），若
a
∥
b
，则实数m的值为（　　）
A、3B、-3C、2D、-2
已知圆M的圆心在x轴上，半径为1，直线l：y=
4
3
x-
1
2
被圆M所截的弦长为
3
，且圆心M在直线l的下方．
（Ⅰ）求圆M的方程；
（Ⅱ）若线段PQ的端点P的坐标为（4，3），端点Q在圆M上运动，线段PQ上一点R满足
PR
=2
RQ
，求R点轨迹方程．
（Ⅲ）设A（0，t），B（0，t+6），（-5≤t≤-2），若圆M是△ABC的内切圆，求△ABC的面积S的最大值和最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网