题目内容
向量a＝(cos 23°，cos 67°)，向量b＝(cos 68°，cos 22°)．
(1)求a·b；
(2)若向量b与向量m共线，u＝a＋m，求u的模的最小值．
解 (1)a·b＝cos 23°·cos 68°＋cos 67°·cos 22°
＝cos 23°·sin 22°＋sin 23°·cos 22°＝sin 45°＝
.
(2)由向量b与向量m共线，得m＝λb (λ∈R)，
u＝a＋m＝a＋λb
＝(cos 23°＋λcos 68°，cos 67°＋λcos 22°)
＝(cos 23°＋λsin 22°，sin 23°＋λcos 22°)，
|u|2＝(cos 23°＋λsin 22°)2＋(sin 23°＋λcos 22°)2
＝λ2＋
λ＋1＝
2＋
，
∴当λ＝－时，|u|有最小值为.
练习册系列答案
相关题目
的两焦点与短轴的一个端点的连线构成等腰直角三角形，直线
与以椭圆C的右焦点为圆心，以
为半径的圆相切。
的右焦点
作直线
交椭圆
于
两点，交y轴于
点，且
求证：
为定值
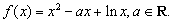
在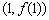
处的切线垂直于
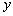轴，求实数a的值；
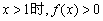恒成立，求实数a的取值范围.
a－b)·c＝30，则x＝________.
＝
＋λ(
＋
)，若λ＝
·(
＋
)的值为______．
与线段AB交于C,且
2
，则实数a=________．
)＋2的图象向右平移
个单位后与原图象重合，则ω的最小值是________．