题目内容
a=(1,2),b=(-3,2),当k为何值时,ka+b与a-3b平行?平行时它们是同向还是反向?
解 方法 一 ka+b=k(1,2)+(-3,2)=(k-3,2k+2),
一 ka+b=k(1,2)+(-3,2)=(k-3,2k+2),
a-3b=(1,2)-3(-3,2)=(10,-4) ,
,
当ka+b 与a-3b平行时,存在唯一实数λ使ka+b=λ(a-3b),由(k-3,2k+2)=λ(10,-4)得,
与a-3b平行时,存在唯一实数λ使ka+b=λ(a-3b),由(k-3,2k+2)=λ(10,-4)得,
 解得k=λ=-
解得k=λ=- ,
,
∴当k= -
- 时,ka+b与a-3b平行,
时,ka+b与a-3b平行,
这时k a+b=-
a+b=- a+b=-
a+b=- (a-3b).
(a-3b).
∵λ=- <0,∴ka+b与a-3b反向.
<0,∴ka+b与a-3b反向.
方法二 由方法一知ka+b=(k-3, 2k+2),
2k+2),
a-3b=(10,-4),∵ka+b与a-3b平行,
∴(k-3)×(-4)-10×(2k+2)=0,解得k=- ,
,
此时ka+b= =-
=- (a-3b).
(a-3b).
∴当k=- 时,ka+b与a-3b平行,并且反向.
时,ka+b与a-3b平行,并且反向.

练习册系列答案
相关题目
 存在唯一零点
存在唯一零点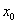 ,则大于
,则大于 与
与 的夹角θ取何值时
的夹角θ取何值时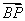 ·
· 的值最大?并求出这个最大值.
的值最大?并求出这个最大值.
 =a,
=a, =b,
=b, =c,则向量
=c,则向量 =____________.
=____________.
 =a,
=a, =b,求
=b,求 ,
, .
. ,b=4
,b=4 ,则B=_____
,则B=_____ ___.
___. 的图象的对称中心是_______________.
的图象的对称中心是_______________.