题目内容
已知函数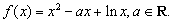
(I)若函数 在
在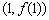 处的切线垂直于
处的切线垂直于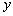 轴,求实数a的值;
轴,求实数a的值;
(II) 在(I)的条件下,求函数 的单调区间;
的单调区间;
(III) 若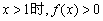 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
解:(I)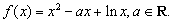 定义域为
定义域为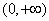
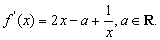
依题意,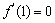 .
.
所以 ,解得
,解得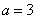 ……………4分
……………4分
(II)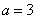 时,
时,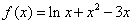 ,定义域为
,定义域为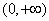 ,
,
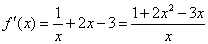
当 或
或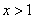 时,
时,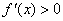 ,
,
当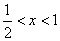 时,
时,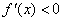 ,
,
故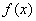 的单调递增区间为
的单调递增区间为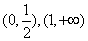 ,单调递减区间为
,单调递减区间为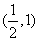 .----8分
.----8分
(III)解法一:由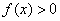 ,得
,得 在
在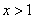 时恒成立,
时恒成立,
令 ,则
,则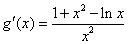
令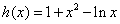 ,则
,则
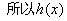 在
在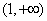 为增函数,
为增函数,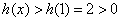 .
.
故 ,故
,故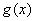 在
在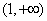 为增函数.
为增函数. 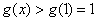 ,
,
所以 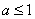 ,即实数
,即实数 的取值范围为
的取值范围为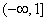 . ……………13分
. ……………13分
解法二: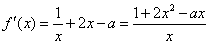
令 ,则
,则 ,
,
(i)当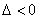 ,即
,即 时,
时,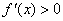 恒成立,
恒成立,
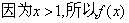 在
在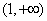 上单调递增,
上单调递增,
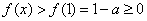 ,即
,即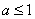 ,所以
,所以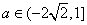 ;
;
(ii)当 ,即
,即 时,
时,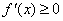 恒成立,
恒成立,
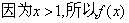 在
在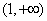 上单调递增,
上单调递增,
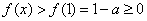 ,即
,即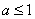 ,所以
,所以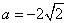 ;
;
(iii)当 ,即
,即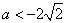 或
或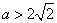 时,
时,
方程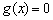 有两个实数根
有两个实数根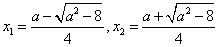
若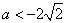 ,两个根
,两个根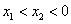 ,
,
当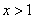 时,
时,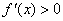 ,
,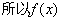 在
在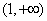 上单调递增,
上单调递增,
则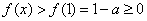 ,即
,即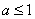 ,所以
,所以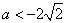 ;
;
若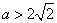 ,
,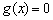 的两个根
的两个根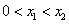 ,
,
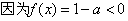 ,且
,且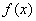 在
在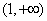 是连续不断的函数
是连续不断的函数
所以总存在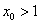 ,使得
,使得 ,不满足题意.
,不满足题意.
综上,实数 的取值范围为
的取值范围为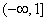 . ……………13分
. ……………13分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,得第n个等式是__________.
中,得第n个等式是__________. 存在唯一零点
存在唯一零点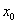 ,则大于
,则大于 B.
B.  C.
C.  D.
D. 

 +
+ -2
-2 )·(
)·(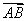 -
- )=0,则△ABC的形状是____________.
)=0,则△ABC的形状是____________. 与
与 的夹角θ取何值时
的夹角θ取何值时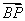 ·
· 的值最大?并求出这个最大值.
的值最大?并求出这个最大值.
 ,b=4
,b=4 ,则B=_____
,则B=_____ ___.
___.