已知下列四个命题:P1:若直线l和平面α内无数条直线垂直.则l⊥αP2:若f(x)=2x-2-x.则?x∈R.fP3:在△ABC中.若A＞B.则sinA＞sinB其中真命题的个数是( )A．0B．1C．2D．3 题目和参考答案——青夏教育精英家教网—

题目内容

2．已知下列四个命题：
P₁：若直线l和平面α内无数条直线垂直，则l⊥α
P₂：若f（x）=2^x-2^-x，则?x∈R，f（-x）=-f（x）
P₃：在△ABC中，若A＞B，则sinA＞sinB
其中真命题的个数是（　　）

A．

B．

C．

D．

分析举例说明命题P₁是假命题；
根据f（x）解析式判断P₂是真命题；
利用正弦定理判断P₃是真命题．

解答解：对于命题P₁，直线l和平面α内无数条直线垂直，则l⊥α不一定成立，
如图所示：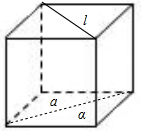

l⊥a，l垂直于α中平行与a的所有直线，但l与α不垂直，P₁是假命题；
对于命题P₂，f（x）=2^x-2^-x，则?x∈R，
f（-x）=2^-x-2^x=-（2^x-2^-x）=-f（x），∴P₂是真命题；
对于P₃，△ABC中，若A＞B，则有a＞b，
由正弦定理知a=2RsinA，b=2RsinB，
∴sinA＞sinB，∴P₃是真命题；
综上，以上真命题的个数是2．
故选：C．

点评本题利用命题真假的判断考查了线面垂直，奇函数以及正弦定理的应用问题，是综合题．

练习册系列答案

相关题目

5．函数y=lg（2cosx-1）的定义域为（　　）

	A．	[-$\frac{π}{3}$，$\frac{π}{3}$]		B．	[2kπ-$\frac{π}{3}$，2kπ+$\frac{π}{3}$]，k∈Z
	C．	（-$\frac{π}{3}$，$\frac{π}{3}$）		D．	（2kπ-$\frac{π}{3}$，2kπ+$\frac{π}{3}$），k∈Z

13．设集合A={2，a}，B={a²-2，2}，若A=B，则实数a=-1．

10．“x＜-2”是“（$\frac{1}{2}$）${\;}^{{x}^{2}}$≥$\frac{1}{16}$”的（　　）