题目内容
已知点A是椭圆
+
=1(a>b>0)上一点,F为椭圆的一个焦点,且AF⊥x 轴,|AF|=焦距,则椭圆的离心率是 .
| x2 |
| a2 |
| y2 |
| b2 |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:通过焦点F的横坐标,代入椭圆方程,求出A的纵坐标,利用|AF|=焦距,结合椭圆中a,b,c的关系,求出椭圆的离心率.
解答:
解:设F为椭圆的右焦点,且AF⊥x轴,所以F(c,0),则
+
=1,解得y=±
,
因为,|AF|=焦距,所以
=2c,即b2=2ac,a2-c2=2ac,
所以e2+2e-1=0,解得e=
-1或e=-
-1(舍去)
故答案为:
-1.
| c2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a |
因为,|AF|=焦距,所以
| b2 |
| a |
所以e2+2e-1=0,解得e=
| 2 |
| 2 |
故答案为:
| 2 |
点评:本题主要考查了椭圆的定义、椭圆的标准方程、椭圆的几何性质,椭圆离心率的求法,属基础题

练习册系列答案
相关题目
 如图,已知正四棱锥S-ABCD的底面边长为2,高为
如图,已知正四棱锥S-ABCD的底面边长为2,高为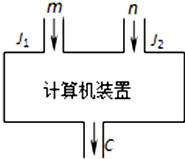 如图是一个计算机装置示意图,J1,J2是数据入口处,C是计算机结果的出口,计算过程是由J1,J2分别输入正整数m和n,经过计算后的结果由C输出.此种计算装置完成的计算满足以下三个性质:
如图是一个计算机装置示意图,J1,J2是数据入口处,C是计算机结果的出口,计算过程是由J1,J2分别输入正整数m和n,经过计算后的结果由C输出.此种计算装置完成的计算满足以下三个性质: