题目内容
已知无穷数列{an}是等差数列,公差为d,前n项和为Sn,则( )
| A、当首项a1>0,d<0时,数列{an}是递减数列且Sn有最大值 |
| B、当首项a1<0,d<0时,数列{an}是递减数列且Sn有最小值 |
| C、当首项a1>0,d>0时,数列{an}是递增数列且Sn有最大值 |
| D、当首项a1<0,d>0时,数列{an}是递减数列且Sn有最大值 |
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:由d的正负易得数列的单调性,由数列项的正负变化入手逐个选项判断即可.
解答:
解:选项A,当首项a1>0,d<0时,数列{an}是递减数列,
数列的前面一些项为正数,从某一项开始为负数,
故Sn有最大值,A正确;
选项B,当首项a1<0,d<0时,数列{an}是递减数列,
数列的所有项均为负数,Sn没有最小值,B错误;
选项C,当首项a1>0,d>0时,数列{an}是递增数列,
数列的所有项均为正数,Sn没有最大值,C错误;
选项D,当首项a1<0,d>0时,数列{an}是递增数列,
数列的前面一些项为负数,从某一项开始为正数,
故Sn有最小值,D错误.
故选:A
数列的前面一些项为正数,从某一项开始为负数,
故Sn有最大值,A正确;
选项B,当首项a1<0,d<0时,数列{an}是递减数列,
数列的所有项均为负数,Sn没有最小值,B错误;
选项C,当首项a1>0,d>0时,数列{an}是递增数列,
数列的所有项均为正数,Sn没有最大值,C错误;
选项D,当首项a1<0,d>0时,数列{an}是递增数列,
数列的前面一些项为负数,从某一项开始为正数,
故Sn有最小值,D错误.
故选:A
点评:本题考查等差数列的前n项和的最值,从数列项的正负变化入手是解决问题的关键,属基础题.

练习册系列答案
相关题目
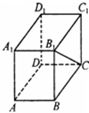
如图,在长方体ABCD-A1B1C1D1中,已知AA1=1,AD=
,则异面直线A1D1与B1C所成角的大小为( )
| 3 |

| A、60° | B、45° |
| C、30° | D、90° |
设x,y满足约束条件
,则z=2x+y的最小值为( )
|
| A、5 | B、8 | C、10 | D、12 |
在△ABC中,已知(a+b+c)(a+b-c)=3ab,则cos(A+B)=( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|