题目内容
如图，在长方体ABCD-A1B1C1D1中，已知AA1=1，AD=
，则异面直线A1D1与B1C所成角的大小为（ ）
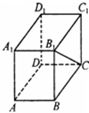
| 3 |
| A、60° | B、45° |
| C、30° | D、90° |
考点：异面直线及其所成的角
专题：空间角
分析：转化异面直线所成角为平面角，通过解三角形即可．
解答：
解：∵A1D1∥B1C1，
∴B1C1与B1C所成的角是∠CB1C1，就是异面直线A1D1与B1C所成角．
∵长方体ABCD-A1B1C1D1中，AA1=1，AD=
，
∴tan∠CB1C1=
=
，
∴∠CB1C1=30°，
∴A1D1与B1C所成的角是30°．
故选：C．
∴B1C1与B1C所成的角是∠CB1C1，就是异面直线A1D1与B1C所成角．
∵长方体ABCD-A1B1C1D1中，AA1=1，AD=
| 3 |
∴tan∠CB1C1=
| CC1 |
| B1C1 |
| ||
| 3 |
∴∠CB1C1=30°，
∴A1D1与B1C所成的角是30°．
故选：C．
点评：本题考查异面直线所成角的求法，是基础题，解题时要认真审题．
练习册系列答案
相关题目
已知一组数1，1，2，3，5，8，x，21，34，55，按这组数规律，x应为（ ）
| A、11 | B、12 | C、13 | D、14 |
已知f（x）=
不等式f（x+a）＞f（2a-x）在[a，a+1]上恒成立，则实数a的取值范围是（ ）
|
| A、（-2，0） |
| B、（-∞，0） |
| C、（0，2） |
| D、（-∞，-2） |
已知在?ABCD中，点M在AB上，且AM=3MB，点N在BD上，且若函数f（x）=
sin（2x+θ）+cos（2x+θ）为奇函数，且在[-
，0]上为减函数，则θ的一个值为（ ）
| 3 |
| π |
| 4 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知无穷数列{an}是等差数列，公差为d，前n项和为Sn，则（ ）
| A、当首项a1＞0，d＜0时，数列{an}是递减数列且Sn有最大值 |
| B、当首项a1＜0，d＜0时，数列{an}是递减数列且Sn有最小值 |
| C、当首项a1＞0，d＞0时，数列{an}是递增数列且Sn有最大值 |
| D、当首项a1＜0，d＞0时，数列{an}是递减数列且Sn有最大值 |